Correlación Vibroacústica: detección cognitiva e identificación de fallas

Resumen

Se presenta una metodología para la investigación diagnóstica de fallas en máquinas industriales mediante un correlador vibroacústico, dispositivo que permite comparar automáticamente las frecuencias de una señal acústica y una vibratoria. Se conjuga así la habilidad humana para la detección de ruidos anómalos con la identificación objetiva de su procedencia.

1. Introducción

El diagnóstico rápido y objetivo de fallas con miras al mantenimiento preventivo suele ser una actividad compleja, especialmente en situaciones en las que se presenta un gran número de equipos en funcionamiento simultáneo cuya interrupción para aplicar protocolos de ensayo no es posible ni conveniente.

Al mismo tiempo, es sabido que el ser humano posee la capacidad de percibir auditivamente diferencias cualitativas bastante sutiles en los sonidos y ruidos presentes en un ambiente determinado, particularmente cuando se produce algún cambio repentino o a corto plazo en ellos. Partiendo de la hipótesis bastante razonable de que dichos cambios pueden ser el primer anuncio de una falla en ciernes, nos encontramos ante la posibilidad de detectar dónde está localizada dicha falla, lo cual implica normalmente una tarea muy laboriosa. Uno de los inconvenientes más grandes está en que las salas de máquinas en la industria o en los edificios suelen ser bastante reverberantes, por lo cual es factible encontrar en todo el recinto sonidos originados en todas las máquinas o fuentes de ruido. Esto dificulta la investigación del origen de ciertas componentes del ruido.

La propuesta que aquí se hace es la de aportar un elemento más para facilitar di-cha búsqueda: las técnicas de correlación vibroacústica. El correlador vibroacústico es un dispositivo que recibe y procesa las señales de dos transductores electromecánicos: un micrófono, que se encarga de recoger la señal acústica (vibraciones que se propagan por el aire), y un acelerómetro, cuyo fin es captar las vibraciones de máquinas y otros objetos con partes sólidas. El procesamiento de estas señales permite determinar si existen componentes frecuenciales idénticas o coherentes en ellas, lo que a su vez permite asociar correctamente el ruido detectado con la máquina (o la parte de ésta) que lo.2 origina. En efecto, en el mundo físico es muy improbable que dos sistemas macroscópicos independientes vibren u oscilen exactamente con la misma frecuencia. Sólo lo harán si se trata de sistemas acoplados o conectados físicamente, como puede serlo una determinada máquina y el aire que la circunda.

2. Teoría del correlador vibroacústico

Dadas dos señales v1(t) y v2(t), se define la función de correlación entre ambas como el promedio a largo plazo del producto entre la primera y la segunda retardada un tiempo t, es decir:

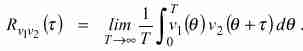(1)

En el caso en que las señales son senoidales de frecuencias w1 y w2, es decir

	(2)
	(3)

sustituyendo en (1) se tendrá

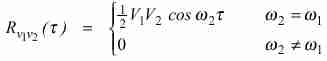(4)

Vemos que la función de correlación sólo es no nula si las dos frecuencias coinciden, es decir, si las dos señales tienen un origen común. Si una de las señales es la salida de un acelerómetro y la otra la de un micrófono, estaremos entonces ante el principio de operación de un correlador vibroacústico.

El esquema anterior presenta el inconveniente de que requiere un tiempo infinito para que pueda apreciarse si existe correlación entre las dos señales. Si se interrumpe el proceso de integración al cabo de un tiempo finito T, para w2 ¹ w1 resulta

	(5)
	(6)
	(7)

	(8)
	(9)

En ambos casos vemos que, para T suficientemente grande, el error puede hacerse arbitrariamente pequeño. Sin embargo, es importante tener en cuenta que, dado que T estará limitado en la práctica a un intervalo de tiempo razonablemente corto (unas pocas decenas de segundo), el error obtenido se traducirá en una incertidumbre acerca de si las frecuencias son iguales o no. En efecto, de (8) puede obtenerse

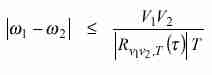(10)

Esta inecuación implica que sólo puede asegurarse que w1 y w2 difieren poco, pero no que sean estrictamente iguales. En muchos casos prácticos una diferencia tan pequeña equivale a que sean iguales, ya que es escasamente probable que dos máquinas independientes generen frecuencias tan similares.

Las inecuaciones (9) y (10) pueden combinarse para obtener

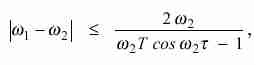(11)

desigualdad válida siempre y cuando el denominador sea positivo, lo cual está sujeto, a su vez, a que t sea pequeño y T grande. En la práctica es necesario hacer el ensayo con varios valores de t, ya que no hay certeza de cuál será el retardo entre la vibración de la máquina y su manifestación como sonido en la posición del micrófono, sin dejar de mencionar también que tanto el acelerómetro como el micrófono pueden tener corrimientos de fase de difícil predicción. El retardo t se consigue interponiendo una red defasadora constituida por un filtro pasatodo con frecuencia central ajustable. El esquema teórico anterior debe ser modificado en la práctica, ya que es complicado efectuar el proceso de integración exacto y luego dividir por el tiempo de integración. Es mucho más sencillo utilizar, a modo de promediador, un simple filtro pasabajos RC para v1(q) v2(q + t). En ese caso la ecuación 1 será reemplazada por 2

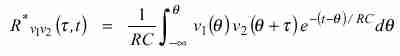(12)

Esta integral representa lo que se denomina una promediación exponencial, o, también, promedio móvil. Intuitivamente, efectúa la promediación dando mayor peso a los valores más recientes del producto v1(q) v2(q + t), siendo el resultado una medida de la correlación “local” (válida en las inmediaciones de t) entre las dos señales. Podemos escribir.4

(13)

donde se aprecian dos componentes: una de baja frecuencia (w2 – w1) y la otra de frecuencia relativamente alta (w2 + w1). El filtro pasabajos puede elegirse de manera que elimine esta última, para lo cual basta tomar RC (w2 + w1) >> 1. Entonces

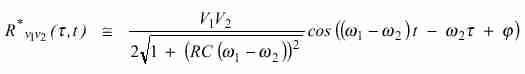(14)

donde j es el defasaje introducido por el filtro, que carece de importancia para nuestro propósito. La correlación local entre las dos señales es, entonces, una onda senoidal de baja frecuencia cuya amplitud es máxima cuando w2 = w1 y decrece al aumentar la diferencia w2 – w1.

Si las amplitudes V1 y V2 fueran constantes y además se conocieran exactamente, con un simple detector de pico podría obtenerse información a partir de la cual determinar w2 – w1 (en caso de ser iguales, sería preciso, además, variar t hasta obtener el máximo valor, equivalente al de pico). Pero en los casos reales, no sólo varían V1 y V2, sino que además las señales de entrada son una compleja superposición de tonos y ruidos de banda ancha. Es necesario, por consiguiente, establecer un criterio que permita discriminar los casos en que existe suficiente correlación entre las señales vibratoria y acústica como para sospechar una relación causal entre ambas. Para ello proponemos, en principio arbitrariamente, un umbral Rmín de correlación por encima del cual considera- remos que la relación causal es probable. Por otro lado, y en función del conocimiento del tipo de máquinas o fuentes de ruido, proponemos una mínima separación de frecuencias Dwmín que permite descartar la interdependencia entre las señales. Si las má- quinas son todas diferentes, por ejemplo, Dwmín podrá ser relativamente grande. Si hay varias máquinas iguales funcionando en regímenes similares, deberá adoptarse un valor mucho menor, ya que es probable que las frecuencias emitidas sean semejantes. Se pretende que aún con una diferencia de frecuencias tan pequeña como Dwmín la amplitud de la correlación local R*v1v2 resulte menor que Rmín, es decir

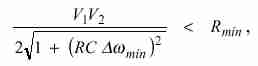(15)

lo cual se logra eligiendo la constante de tiempo del filtro pasabajos de modo que

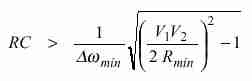(16)

De esta forma, estaremos seguros de que si se supera el umbral de correlación la diferencia de frecuencias es menor que Dwmín, y por consiguiente la interdependencia es probable. Vemos que cuanto más seguridad pretendamos tener (es decir, cuanto más pequeño sea Dwmín), mayor ha de ser la constante de tiempo, lo cual se traduce en un mayor tiempo de medición. En general es necesario adoptar un compromiso entre la practicidad (rapidez) de la medición y las garantías de un diagnóstico acertado..5 Hasta ahora hemos analizado el caso en que las señales v1(t) y v2(t) eran ambas senoidales. En un caso general, podrán ser la suma de diversas componentes tonales (armónicas o inarmónicas):

	(17)
	(18)
	(19)

La correlación local obtenida por medio de un filtro pasabajos es, despreciando aquellas componentes que se encuentran por encima de 10/RC,

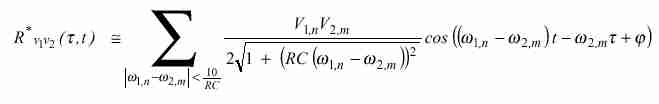(20)

cuyo valor eficaz (RMS) es

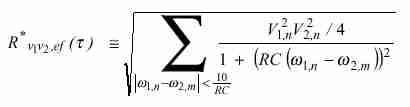(21)

Es evidente que en general existen demasiadas componentes en esta expresión, lo cual puede llevar a que el umbral Rmín sea superado globalmente sin que individual- mente haya componentes de igual frecuencia en ambas señales. Por ese motivo es conveniente, antes de efectuar la correlación, filtrar ambas señales con sendos filtros de bandas, de manera de reducir la cantidad de componentes a correlacionar.

3. Estructura del correlador vibroacústico

La estructura requerida para implementar el correlador vibroacústico se ilustra en la figura 1. Consta de los transductores con sus respectivos preamplificadores de ganancia ajustable. Es importante que éstos sean de bajo ruido propio ya que las componentes coherentes de la aceleración y la presión sonora podrían ser de bajo nivel. También es crítico que tengan un elevado rechazo a la fuente de alimentación, ya que de lo contrario podrían contener la frecuencia de la línea de distribución eléctrica (50 Hz ó 60 Hz) o sus armónicos, creando una falsa coherencia que sería detectada por las etapas posteriores del correlador. Los filtros pasabanda están sintonizados a igual frecuencia, y podrían ser de bandas de octava o de tercio de octava, con frecuencia central seleccionable por el usuario. El retardo puede implementarse con un filtro pasatodo de primer orden cuya frecuencia central (aquélla a la cual desfasa 90º) sea ajustable, ya sea manual o automáticamente, por pasos o en forma continua. Los auriculares permiten al operador determinar si el ruido anómalo permanece o es eliminado por el filtro pasabanda. Debería seleccionarse la frecuencia del pasabanda de manera que el ruido en cuestión o parte de él se conserve. El multiplicador es de 4 cuadrantes y de gran rango dinámico, lo cual excluye los que utilizan amplificadores logarítmicos y antilogarítmicos. La constante de tiempo RC del filtro pasabajos deberá ser ajustable por pasos desde valores pequeños (por ejemplo 0,1 s) hasta muy grandes (por ejemplo 100 s o más). Esto permite acomodar el tiempo de medición según los requisitos de precisión (error máximo admisible en la diferencia de frecuencias para considerarlas iguales). Finalmente, la salida del detector de valor eficaz se compara con el umbral, dando una indicación positiva en caso de superarse éste.

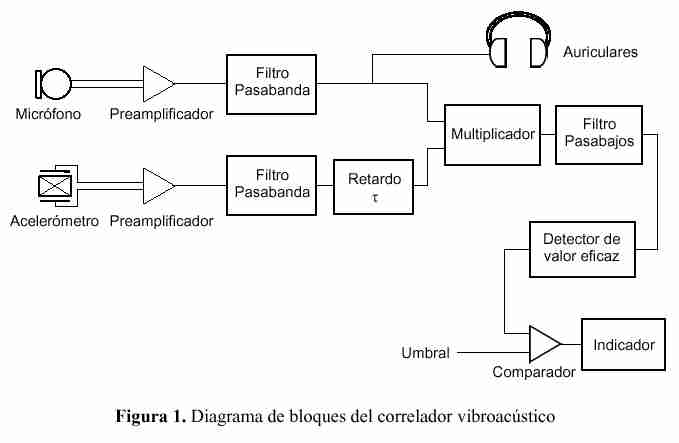El diagrama anterior ha sido implementado, con algunas variantes, como proyecto de una asignatura de la carrera de Ingeniería Electrónica de la Universidad Nacional de Rosario, con tecnología electrónica analógica.3 Como acelerómetro se utilizó el ADXL105, un circuito integrado monolítico micromaquinado de muy bajo costo. También podría utilizarse una estructura basada en procesadores digitales de señal (DSP) o una plataforma computacional de cualquier tipo (por ejemplo, una computadora personal), tanto en tiempo real como en tiempo diferido (previa adquisición de datos mediante tarjeta digitalizadora), dependiendo de la potencia de la plataforma y el software. Dado que una gran mayoría de las vibraciones son periódicas o cuasiperiódicas, se podría mejorar la estructura anterior reemplazando los filtros pasabanda por filtros peine (comb filters), es decir filtros que tienen una estrecha banda de paso sobre cada armónico de una serie cuya fundamental sería, en este caso, ajustable. Con tecnología analógica esto no resulta práctico, pero con tecnología digital sí. Aunque aún no se ha implementado en la práctica esta idea, tendría la ventaja de individualizar no sólo frecuencias aisladas, sino todas las frecuencias asociadas a una determinada falla o anomalía, con lo cual la detección sería más consistente.

4. Metodología

La metodología de trabajo propuesta se inserta dentro del marco del mantenimiento preventivo. El personal afectado al área de trabajo, particularmente el personal de supervisión, debe estar instruido para informar sobre cualquier cambio que se produzca en los ruidos y sonidos ambientes. Paralelamente, es muy conveniente efectuar periódicamente una grabación digital del ruido ambiente en condiciones normales de operación y en diferentes posiciones cuidadosamente documentadas, para comparación ulterior. Las mismas se guardarán en soporte óptico (CD-ROM o Minidisc), dado que es el que mayor durabilidad e inalterabilidad ofrece.

Una vez detectada una anomalía acústica se procederá a efectuar un análisis mediante el correlador vibroacústico descripto. Para ello se procederá a circunscribir es-pectralmente la anomalía, para lo cual deberá seleccionarse una banda filtrante en la cual pueda escucharse aún claramente la anomalía. La audición de la grabación original (sin anomalías) puede servir como referencia y utilizarse alternativamente para seleccionar la banda más representativa. Esta selección es muy importante porque existen numerosos ruidos en el ambiente que se correlacionarán con las vibraciones de diversas máquinas, por lo cual podrían recogerse resultados positivos falsos o espurios. El filtro permite descartar aquéllos que pertenecen al ruido ambiente normal.

Luego se investigará cada máquina o fuente de ruido por separado, teniendo en cuenta algunas precauciones en la ubicación del acelerómetro, ya que ciertas vibraciones son muy notorias en algunas direcciones pero casi nulas en otras. En principio debe suponerse que las grandes superficies (tales como cubiertas de protección) se comportan como radiadores principales, pero en algunos casos la radiación puede producirse desde una superficie cuya vibración es estimulada por la vibración de la máquina por vía sólida.

Debido a fenómenos modales, podría inclusive haber ciertos puntos de una superficie que es encuentran en reposo (por ejemplo sobre las líneas nodales), mientras en otros ello no sucede. Es importante observar que ello podría ocurrir precisamente para las frecuencias coherentes, y por lo tanto perderse éstas. Por ello debe probarse en dos o tres posiciones. Puede intentarse primero efectuar determinaciones rápidas pero más imprecisas utilizando una constante de tiempo corta. Un resultado negativo permite descartar la posición ensayada, pero uno positivo requerirá nuevos ensayos con una mayor constante de tiempo.

El estudio se considerará terminado cuando se encuentre una máquina o parte de ella que arroje resultados positivos con la máxima constante de tiempo. Entonces se podrá proceder a verificar y corregir la falla sometiendo la máquina a tareas de mantenimiento.

Es importante tener en cuenta la participación en todo momento de personal conocedor de las máquinas, que permitirá resolver situaciones que vayan surgiendo en los ensayos. Por el momento esta técnica no es susceptible de ser automatizada a un costo razonable.

Referencias

[1] Gerges, Samir: “Ruido: Fundamentos y Control”. Edición del autor. Florianópolis, Brasil,1998.

[2] Beranek, Leo: “Acoustical Measurements”. American Institute of Physics, Acoustical Society of America. Woodbury, USA, 1988.

[3] Gallegos, José Luis; Devigli, Mauro; Colacrai, Nicolás: “Correlador Vibroacústico”.Proyecto de la asignatura Electrónica Lineal II, carrera de Ingeniería Electrónica.Universidad Nacional de Rosario, 1999. ([email protected])

Ing. Federico Miyara
Laboratorio de Acústica y Electroacústica
Universidad Nacional de Rosario