Modelizado y simulación del viento efectivo experimentado en turbinas eólicas

RESUMEN: El grado de desarrollo que han alcanzado las turbinas eólicas de elevada potencia hace necesario la aplicación de modelos realistas de viento que permitan evaluar su comportamiento dinámico desde las primeras etapas de diseño y simulación. En efecto, a pesar de la mejora continua de los pronósticos meteorológicos también se torna indispensable determinar de manera fehaciente el viento efectivo que “ven” las turbinas de alta potencia considerando la implicancia en la
generación de energía.

En este sentido, a partir de la aplicación de diversos enfoques, se puede realizar una aproximación de la velocidad de viento que, finalmente, se transforma en potencia eléctrica pero además la manera en que la extracción de la potencia eólica perturba a la potencia eléctrica producida en virtud de las características del proceso de transformación de energía.
Luego, este trabajo presenta resultados de simulación que permiten inferir no solamente la velocidad de viento que, efectivamente, ven las turbinas modernas sino el efecto sobre la red eléctrica considerando un generador tipo jaula de ardilla.

Palabras clave: viento efectivo, velocidad media, turbulencia, perfil de viento, sombra de la torre, turbina eólica.

1. INTRODUCCIÓN

En los aerogeneradores y las granjas eólicas modernas el correcto modelado de la velocidad del viento es de fundamental importancia porque permite la predicción de la producción de energía, el análisis de la conversión de la energía, la dinámica de los sistema, etc.

Este trabajo involucra al segundo de los puntos citados, es decir, el análisis de la conversión de energía desde el punto de vista de la red eléctrica a la cual se encuentran conectados los aerogeneradores. En ese sentido, se comienza por el modelado de la velocidad del viento que se transforma en energía eléctrica para luego acoplarlo al modelo de un aerogenerador moderno. De esta manera, se pretenden reproducir los distintos fenómenos que aportan potencia pero a la vez polucionan la red eléctrica considerando el proceso que da lugar a la generación.

Para analizar la conversión de energía, se hace necesario establecer herramientas que permitan predecir el efecto del viento sobre los aerogeneradores modernos tanto desde el punto de vista de la generación propiamente dicha como desde el punto de vista de las cargas estructurales, que aparecen a consecuencia de diversos efectos.

Para el modelo matemático del viento se describen tanto los procesos estocásticos como los determinísticos junto con procesos de dinámicas más lentas como la evolución del valor medio del viento. A partir de obtener el viento efectivo se establecen los restantes modelos físicos del eje de transmisión y el generador eléctrico los que se combinan para obtener el citado efecto sobre la red eléctrica.

Por lo anterior, se considera para la etapa de generación a una máquina ampliamente conocida, el generador tipo jaula de ardilla, a los efectos de evaluar la manera en que se impacta sobre la red eléctrica con la generación eólica.

El trabajo se encuentra estructurado de la siguiente manera: en la Sección 2 se modela al viento a partir de analizar por separado a las componentes del mismo y considerando la manera en que las turbinas eólicas extraen la energía. En la Sección 3 se presenta el modelo de una turbina moderna mientras que en la Sección 4 se presentan resultados de simulación en los que resalta el efecto sobre la red eléctrica bajo condiciones de viento reales. Finalmente, la última sección presenta las conclusiones.

2. VELOCIDAD DE VIENTO QUE EXPERIMENTA LA TURBINA Y SU MODELADO

La distribución de velocidad está lejos de ser uniforme en toda el área barrida por las palas de una turbina eólica; las velocidades de viento medidas en diferentes puntos de dicha área pueden variar considerablemente, tanto en su componente media como en la componente turbulenta. Como consecuencia de esta distribución espacial, la cual se puede considerar constante para el tiempo que tarda en dar una vuelta el rotor, un elemento de pala experimentará diferentes velocidades del viento a medida que gira, generando una señal periódica con frecuencia fundamental igual a la velocidad de rotación. Esta frecuencia se denota como 1P (Bianchi et al., 2007). La fluctuación de la velocidad del viento experimentado por un punto de rotación produce perturbaciones cíclicas en la fuerza de empuje aerodinámico y en el par de giro que deben ser soportados por las palas. Además, algunas componentes de frecuencia de estas perturbaciones se propagan por el tren de tracción y la estructura. Estas cargas aerodinámicas tienen un impacto directo en el costo de energía porque reducen la vida útil de los aerogeneradores y deterioran la calidad de la potencia suministrada a la red eléctrica.
La velocidad del viento en un punto fijo puede ser dividida en una velocidad media cuasi-estacionaria y la turbulencia (Bianchi et al., 2007), donde la velocidad media se determina típicamente como un promedio en períodos de 10 a 20 minutos. Por lo anterior, se puede considerar la velocidad media del viento como constante durante varias revoluciones del rotor, pero la variación de la velocidad en un elemento de pala que gira se puede separar en una componente determinista y una estocástica.

2.1 Componentes determinísticas del viento.

2.1.2 El perfil del viento con la altura

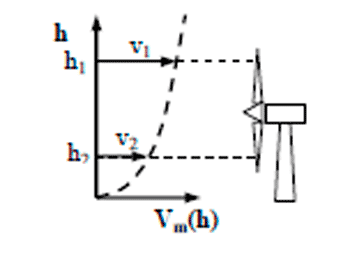
El aumento de la velocidad media del viento con la altura es causa de cargas aerodinámicas variables. De hecho, el gradiente de velocidad media produce una variación cíclica en la velocidad del viento experimentada por un elemento de la pala siendo mayor en la punto superior del barrido de las palas e inferior en el punto más bajo (Fig.1).

La velocidad a una determinada altura puede estimarse por (Freris, 1990; Panofsky, 1987):

Donde h es la altura del eje, hr es la altura de un elemento de pala, y z0 es la longitud característica de la rugosidad del terreno (Freris, 1990; Panofsky, 1987).
La fluctuación del par de cada pala es casi sinusoidal con una frecuencia del valor del giro de la pala. Debido al efecto del promedio de las palas, solo la frecuencia 3P y armónicos se propagan mientras que el componente fundamental se cancela.
Así, las cargas aerodinámicas sobre las palas son significativamente atenuadas cuando se transmiten a través del dispositivos restantes del tren de transmisión.

2.1.3 La sombra de la torre

Las turbinas de eje horizontal son soportadas por torres que pueden ser tubulares en el caso de pequeñas turbinas y son cilíndricas para las grandes. Las torres son obstáculos que afectan a apreciablemente el flujo de aire. En dicho flujo las líneas de corriente se apartan justo enfrente de la torre. Luego, el flujo de aire pasa a poseer una velocidad lateral Vx que antes no tenía, mientras que se reduce su velocidad axial Vy. Este efecto se llama sombra de la torre (Fig.2).

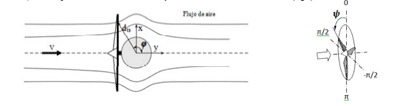Efecto de la sombra de la torre en el flujo de aire.

Las ecuaciones para Vx y Vy se muestran a continuación (Bianchi et al., 2007)

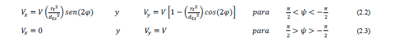La transformada rápida de Fourier se representa en la parte inferior de la figura revela que el energía se extiende sobre una amplia gama de frecuencias. Se observa que la componente 3P es más apreciable que en el efecto cortante del viento. En general, la sombra de la torre es la carga determinista más importante (Fig.3) (Bianchi et al., 2007).

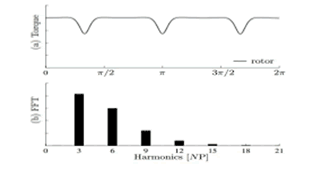Efecto de la sombra de la torre pana una turbina de 3 palas (N=3) (a) Fluctuaciones del par del rotor (b) Transformada rápida de Fourier

Vale la pena mencionar que la “sombra” causada por otros obstáculos, como la vegetación y la topografía del lugar, edificios u otras turbinas eólicas, tiene efectos similares y puede ser tratada del mismo modo, aunque la cuantificación puede resultar mucho más complicada.

2.2. Componente estocástica del viento

Además de las fluctuaciones deterministas, hay una variación estocástica de la velocidad del viento. Dado que el espectro de turbulencia puede ser estimado estadísticamente a partir de mediciones meteorológicas, es posible considerar que en toda el área de barrido en cada instante de tiempo existe una componente del viento que pertenece a la turbulencia y que impacta en la potencia que se traslada al eje de la turbina. En las turbinas eólicas modernas, la frecuencia de giro del rotor es varias veces superior al ancho de banda de la turbulencia; de esta manera, la distribución de turbulencia sobre el disco del rotor puede considerarse constante en cada vuelta de giro del mismo (Bianchi et al., 2007).

En efecto, como la variación temporal de la velocidad del viento debido a la turbulencia es mucho menor que la velocidad de giro de las palas, se considera que la turbulencia se mantiene fija (“congelada”) para cada vuelta del rotor de la turbina. Así, el efecto de la turbulencia sobre las palas posee componentes que se concentra alrededor de la frecuencia de giro y sus armónicos. Luego, el espectro del viento experimentado por las palas está alrededor de la frecuencia de giro de cada pala y sus armónicos. Por lo tanto, el par aerodinámico desarrollado por el rotor completo tendrá fluctuaciones apreciables de frecuencias alrededor de NP (Sørensen, 1990).

2.3. Modelo de viento efectivo

Como se comentó al inicio del punto 2, la distribución de velocidad del viento está lejos de ser uniforme en toda el área barrida por las palas de un aerogenerador. Además, como hemos visto en 2.1 y 2.2, la velocidad del viento en un punto fijo puede considerarse como la suma de dos componentes, el valor medio cuasi-constante asociado a las variaciones lentas, y la turbulencia asociada a las variaciones rápidas. Si consideramos la velocidad de viento experimentada por un punto que gira, un tercer componente puede ser incluido para tener en cuenta el efecto de muestreo de rotación.

Así, se puede construir un campo de viento tridimensional, dividiendo al área barrida por las palas en sectores, cada uno de ellos caracterizado por una señal de velocidad del viento distinta, predecir las fuerzas que actúan sobre cada elemento de pala para un instante dado, y sumando todas ellas determinar la fuerza total, y por lo tanto el par en ese instante de tiempo. Esto implica un volumen de cálculo excesivo (Sørensen, 1990).

Una alternativa más simple consiste en obtener una velocidad escalar de viento ficticio, a la que llamaremos velocidad de viento eficaz, que genera un efecto equivalente al efecto total producido por el campo de velocidad de viento tridimensional sobre cada elemento de pala de toda la turbina.

Resumiendo, la velocidad del viento eficaz puede ser considerada como la velocidad del viento escalar con la que se obtiene el mismo par aerodinámico que el conseguido con el campo de viento tridimensional velocidad aplicado a cada elemento de pala.

El modelado de la velocidad del viento efectivo está básicamente dividido en dos partes, el modelado de la velocidad de viento media y el modelado de la turbulencia. Tanto el efecto de muestreo de rotación en la turbulencia como el perfil del viento y la sombra de la torre se incorporan en el segundo. (Fig.4)

2.3.1 Modelo de turbulencia

La turbulencia se describe por su espectro de potencia, que está completamente caracterizado por la longitud de correlación, la intensidad de la turbulencia y la velocidad media del viento. Por lo tanto, un modelo de turbulencia puede ser construido haciendo pasar ruido blanco W(t) a través de un filtro de paso bajo que tienen la respuesta de frecuencia del espectro de potencia. Para el espectro de Von Karman, el filtro de paso bajo es de orden fraccional, por lo que para reducir el tiempo de calculo se aproxima utilizando un filtro racional, por ejemplo uno de segundo orden de la forma (Bianchi et al., 2007)

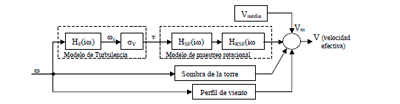Diagrama en bloques del modelo de viento efectivo

2.3.2 Modelo de muestreo rotacional

Una vez calculada la turbulencia a la altura del eje, se la pasa a través de un par de filtros. El primero, llamado filtro espacial, atenúa los componentes de alta frecuencia de la turbulencia. Una expresión factible para este filtro es

donde ωSF es la frecuencia de corte, que depende de la velocidad media del viento y la intensidad de turbulencia (Welfonder et al., 1997). El segundo filtro modela el efecto del muestreo de rotación. Una expresión razonable para este filtro es

donde el coeficiente de amortiguamiento d es función de la velocidad media del viento, la intensidad de la turbulencia y la frecuencia de rotación. Este filtro amplifica las componentes con frecuencias próximas a NP. Filtros similares se pueden añadir para amplificar armónicos más altos.

3. MODELO DE TURBINA EÓLICA

Para reflejar adecuadamente el comportamiento dinámico de una turbina eólica moderna de eje horizontal y paso de pala variable se analizan los componentes principales y sus características de acuerdo al diagrama de bloques Fig.5 . En lo que sigue de esta sección, excepto el sistema de control y el actuador de paso de palas debido a que se simulará para velocidades de viento inferiores a la nominal (por lo tanto, β=0), se presentará el modelo matemático de las partes indicadas en la mencionada figura.

3.1 Modelo Aerodinámico de la turbina.

Es bien conocido que, parte de la energía contenida en el viento se transforma en energía mecánica al atravesar las palas del rotor (Freris, 1990; Burton et al., 2001). La potencia media transferida al eje de la turbina viene dada por

Donde:
ρ: densidad del aire (Kg/m3), Ar = π.R2 : área barrida por las palas del rotor (m2), R: largo de las palas (m), Cp(λ,β): coeficiente de potencia aerodinámico, Vviento: velocidad media de viento incidente (m/s), β: ángulo de paso de pala respecto al viento (º), y λ: relación entre la velocidad de viento y la velocidad de punta de pala dada por:

siendo ωm la velocidad angular de la turbina (rad/seg).

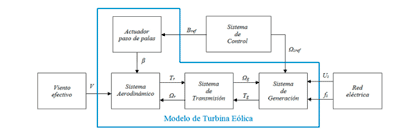
Fig.5 Estructura General del Modelo de Turbina Eólica

Asimismo, el par mecánico en el eje de la turbina esta dado por la siguiente relación:

Donde CT(λ,β) es el coeficiente de par aerodinámico dado por :

El coeficiente CP(λ,β) denota la performance de la turbina respecto a la potencia teórica máxima que se podría obtener del
viento. Por lo general su dependencia del ángulo de paso de palas β y de la relación λ se obtiene por ensayo de la máquina
eólica. Este coeficiente se presenta en el anexo.

3.2 Sistema Mecánico de Transmisión

Este sistema, descrito gráficamente en la Fig.6 se compone de un eje acoplado al rotor eólico que transmite el movimiento de rotación al generador eléctrico. Puesto que en general los generadores trabajan a velocidades superiores a la de la turbina, se intercala una caja multiplicadora de relación N y alto rendimiento que adapta la potencia transmitida por el rotor en términos de par y velocidad angular. El eje de alta velocidad entre la caja multiplicadora y el generador se modela como un elemento flexible representado por un resorte de torsión de rigidez KS y amortiguamiento BS. A partir de utilizar las leyes de Newton para resolver el sistema de la Fig.6, se obtienen tres ecuaciones de estado que representan la dinámica del sistema mecánico de transmisión.

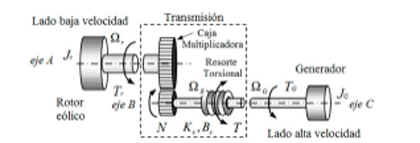Modelo de transmisión mecánica de 2 masas.

3.3 Sistema de Generación Eléctrica

Este sistema recibe la potencia mecánica de la salida de la caja multiplicadora y la convierte en energía eléctrica que se inyecta a la red. Uno de los generadores eléctricos ampliamente utilizados en la industria eólica es la maquina asincrónica de inducción tipo ”jaula de ardilla” (SCIG), directamente conectado a la red eléctrica. En este esquema, denominado de velocidad fija, la tensión US y la frecuencia fS en bornes del generador son impuestas por la red. El modelo que describe el comportamiento eléctrico es (Petru y Thringer, 2002; Krause et al., 2002):

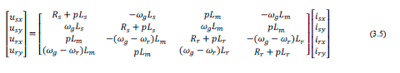Donde usx, usy e isx, isy son las tensiones y corrientes estatóricas en un marco de referencia rotante general x-y que gira a velocidad sincrónica ω1. Idénticas consideraciones se mantienen para las cantidades rotóricas. Además, p es el operador derivada temporal, los subíndices s indican cantidades estatóricas, r las rotóricas, R son las resistencias y L las inductancias, a su vez, el subíndice m indica magnetización mientras que S es el resbalamiento de la máquina. Por otro lado, el par eléctrico es:

Siendo P la cantidad de pares de polos.

4. SIMULACIONES

En la Fig.7 se presenta el sistema bajo estudio. El mismo consta de un aerogenerador, cuyos datos se adjuntan en el ANEXO, que se conecta al resto de la red eléctrica por medio de una línea de transmisión; se modeló y simuló con el software Simulink de MATLAB.

Sistema bajo estudio.

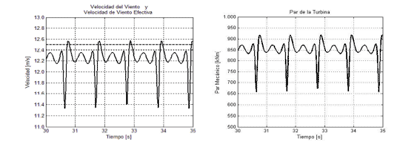
La Fig.8 muestra, para una velocidad de viento real de 12,5 m/s (línea de trazos) que se puede considerar constante como se indicó en el punto 2, la velocidad efectiva obtenida del modelo presentado en la Fig.4. La velocidad efectiva es, como fue desarrollado en 2.3, la velocidad del viento escalar con la que se obtienen los mismos par aerodinámico y potencia mecánica que los conseguidos mediante la sumatoria de los efectos producidos por el campo de velocidad de viento tridimensional aplicado a cada elemento de pala. Surge de aplicarle al viento real los efectos de la turbulencia, el perfil de viento y la sombra de la torre.

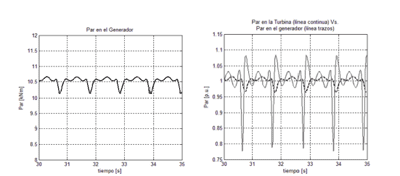
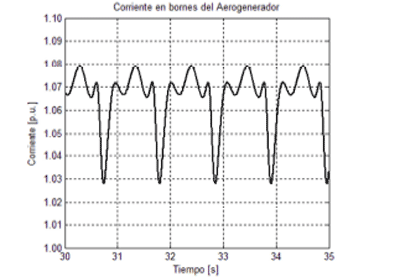
Las Fig.9 y 10 presentan el par en el eje de la turbina eólica y el par en el generador eléctrico, y en la Fig.11 vemos la comparación de ambas, donde se aprecia el efecto amortiguador del modelo de dos masas del tren mecánico. Por otra parte la Fig.12 presenta la corriente producida por el aerogenerador.

Perfil de viento efectivo obtenido del modelo de la Fig.4 Par mecánico en el eje de la Turbina. Par mecánico en el Generador Pares de la Turbina y el Generador [p.u.] Corriente en bornes del Generador Aún cuando entre las Fig. 8 y 9 se observa una atenuación en el par que experimenta la turbina producto de la flexibilidad del eje rápido y el amortiguamiento del mismo, en la Fig.12 podemos ver cómo la perturbación producto del par pulsante se traslada a la corriente generada de manera de perturbar a la red eléctrica en la que se está aportando energía. Esta variación de corriente da lugar a fluctuaciones de tensión en la línea de conexión, o efecto flicker (Larsson, 2002; Sørensen et al., 1996). 5. CONCLUSIONES Se ha presentado el modelado del viento efectivo, teniendo en cuenta tanto las componentes determinísticas como el efecto del perfil vertical de viento y la sombra de la torre, como la componente estocástica o turbulencia. La máquina eólica se ha modelado como dos masas concentradas vinculadas por medio de un eje rápido flexible y se ha considerado que el generador eléctrico es del tipo asincrónico jaula de ardilla. Se han realizado simulaciones bajo la condición de velocidad de viento constante para determinar el viento efectivo, y así obtener las características de las variables mecánicas y eléctricas del aerogenerador, y como se ve afectada la red eléctrica a la cual está conectada. Las simulaciones muestran que se ha reproducido el efecto de flicker observado en los aerogeneradores modernos ampliamente citado en la bibliografía. Si bien los resultados se han obtenido a partir de la conjunción de distintos modelos presentados en bibliografía conocida, a los efectos de verificar la frecuencia de variación y el efecto de cada componente, a futuro y en virtud de un convenio de trabajo existente, se prevé comparar el modelo obtenido con los datos experimentales que se tendrán del aerogenerador NRG1500 que se encuentra en funcionamiento en la zona de Comodoro Rivadavia. Además, se prevé la utilización del modelo obtenido para estudiar métodos de reducción de perturbaciones en redes débiles debidas a la conexión de aerogeneradores dado que en dichas redes la tensión se ve fuertemente afectada por la condición pulsante de la corriente. 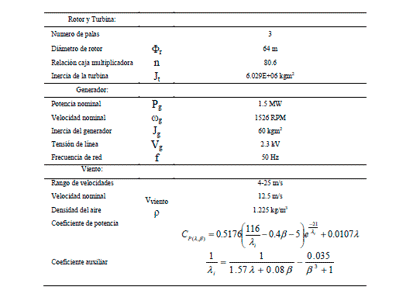REFERENCIAS Bianchi, F.D. DeBatista, H. y Mantz, R.J. (2007). “Wind Turbine Control Systems. Principles, Modelling and Gain Scheduling Design”, Springer. Freris, L. (1990). “Wind Energy Conversion Systems”, Prentice-Hall internacional. Panofsky, H. (1974). “The atmospheric boundary layer below 150 metres”. Annual Review of Fluid Mechanics. Sørensen, P. (1995). “Methods for calculation of flicker contributions from wind turbines”. Technical Report RISO-I- 939(EN), Risø National Labo-ratory, Roskilde, Denmark. Welfonder, E., Neifer, R. y Spanner, M. (1997). “Development and experimental identification of dynamic models for wind turbines”. Control Engineering Practice. Burton, T.; Sharpe, D.; Jenkins N. y Bossanyi, E. (2001). “Wind Energy Handbook”. Wiley & Sons Ltd. Petru, T. and Thringer, T. (2002). “Modeling of wind turbines for power system studies”. IEEE Transactions on Power Systems 17(4), 1132–1139. Krause, P.C.; Wasynczuk O. y Sudhoff S.D. (2002). “Analysis of electric machinery and drive systems”. IEEE Power Engineering Society Sørensen, P. et al. (1996), “Flicker emission levels from wind turbines”, Wind Eng. , vol. 20, No. 1. Larsson, A. (2002). “Flicker Emission of Wind Turbines During Continuous Operation”. IEEE Transactions on Energy Conversion, vol. 17, No. 1. ANEXO: TURBINA EÓLICA Los parámetros de diseño de la turbina que se utilizan en la etapa de simulación pueden verse resumidos en la Tabla 1. Tabla 1. Datos principales de la turbina eólica. Por: Gerardo Ahrtz, Alejandro Münnemann, Daniel Fernández

VER ARCHIVO DE ARTÍCULOS