Cristalografía – 2º Parte

Sistemas Cristalinos

Conocidos los elementos de simetría podemos hablar de ejes cristalográficos   y cruz axial.

Los ejes cristalográficos son líneas imaginarias que se cruzan en el centro de simetría y sirven para ubicar las distintas caras del cristal en el espacio.

Generalmente  coinciden con los ejes de simetría y en su intersección forman la cruz axial.

La cruz axial responde a una relación angular y de longitud entre los ejes cristalográficos.

En la cruz axial los ejes cristalográficos se denominan, convencionalmente, “a”, “b” y “c” y los ángulos que forman entre sí: alfa, beta y gama. Ver Fig. 1

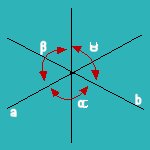
Figura 1

De acuerdo a estas relaciones se definen seis (6) sistemas cristalinos.

Luego, para una mejor visualización, definiremos cada sistema con una figura, la relación de ejes y ángulos y un ejemplo de mineral.

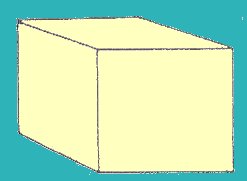
Sistema Cúbico (Fig. 2)

Cristales que como máximo tienen los siguientes elementos de simetría:

3 ejes cuaternarios – 4 ejes ternarios – 6 ejes binarios – 9 planos de simetría y 1 centro de simetría.

Su cruz axial responde a la siguiente relación:

“a” = “b” = “c” / alfa = beta = gama.

Ejemplos: Pirita (FeS2) – Diamante (C), etc.

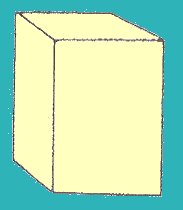
Sistema Tetragonal  (Fig. 3)

Cristales que como máximo tienen los siguientes elementos de simetría:

1 eje cuaternario – 4 ejes binarios – 5 planos de simetría – 1 centro de simetría

Su cruz  axial responde a la siguiente relación:

“a” = ”b” distinto de “c”  /  alfa = beta = gama

Ejemplo: Calcopirita (FeCuS2)

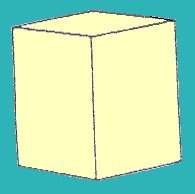
Sistema Rómbico  (Fig. 4)

Cristales que como máximo tienen los siguientes elementos de simetría:

3 ejes binarios – 3 planos de simetría – 1 centro de simetría

Su cruz axial responde a la siguiente relación:

“a” distinto de “b” distinto de “c”  /  alfa = beta =gama

Ejemplo: Baritina  (BaSo4)

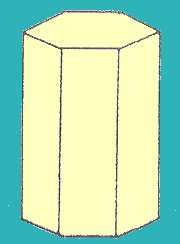
Sistema Hexagonal (Fig. 5)

Cristales que como máximo tienen los siguientes elementos de simetría:

1eje senario o ternario – 6 ejes binarios – 7 planos de simetría 1 centro de simetría

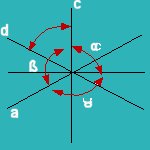
Figura 6

Su cruz axial es diferente (Fig. 6) a las anteriores ya que aquí aparece otro eje cristalográfico0: el eje “d” y otro ángulo “delta”. Su relación es:

“a” = ”b” = ”d” distinto de ”c”  /  beta  = gama = delta distinto de alfa

Ejemplo: Berilo  (Be3Al2Si6O18)

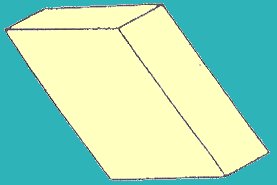
Sistema Monoclínico  (Fig. 7)

Cristales que como máximo tienen los siguientes elementos de simetría:

1 eje binario – 1 plano de simetría – 1 centro de simetría

Su cruz axial responde a la siguiente relación.

“a” distinto de “b” distinto de “c”  /  alfa = gama distinto de beta

Ejemplo: Ortosa  (KAlSi3O8)

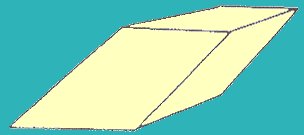
Sistema Triclínico  (Fig. 8)

Estos cristales solo tienen un centro de simetría.

Su cruz  axial responde a la siguiente relación:

“a” distinto de  ”b” distinto de ”c”  /  alfa distinto de beta distinto de gama

Ejemplo: Microclino  (KalSi3O8) de igual fórmula química que la ortosa.

Para finalizar es dable aclarar que estos son ejemplos sencillos y didácticos ya que, en la naturaleza, suelen aparecer cristales de formas tan complicadas que los diferentes autores aún no se ponen de acuerdo en la cantidad y tipos de sistemas.

Geólogo Ricardo Timón