Tendencias en el aislamiento de impactos
 |
RESUMEN
El problema de vibraciones generadas por impactos y choques es una situación común, cuyos efectos suelen ser bastante perjudiciales debido a los altos niveles de aceleración y las grandes deformaciones producidas. El diseño y selección de aisladores es crucial para la minimización de los efectos negativos, sin embargo la investigación sobre impactos es considerablemente menor si se le compara con los estudios existentes en vibración armónica y aleatoria. Es necesario, por lo tanto, proponer nuevas alternativas para el aislamiento adecuado de impactos, principalmente mediante el uso de materiales y estructuras inteligentes que puedan adaptarse a distintas situaciones. El objetivo de este artículo es hacer una revisión de los medios clásicos para el control de impactos, y proponer nuevas estrategias que puedan tener aplicación en el futuro. PALABRAS CLAVE |
INTRODUCCIÓN
El término “vibración transitoria” se refi ere a una excitación temporal en un sistema mecánico. Los impactos y choques son ejemplos de vibración transitoria no periódica, que normalmente se caracterizan por ser aplicados repentinamente, tener una alta severidad, y ser de corta duración. Impactos causados por diferentes fuentes son encontrados normalmente en la vida cotidiana, por ejemplo aquellos causados por prensas, troqueladoras, caída libre de objetos, automóviles pasando por topes, etc.
Este tipo de vibraciones suelen ser bastante dañinas en muchos aspectos, principalmente por su naturaleza no periódica y porque normalmente se ven involucrados altos niveles de aceleración, y grandes deformaciones, que hacen que su control y aislamiento efectivo se vuelvan complicados. Lo anterior hace necesario el desarrollo de nuevas técnicas para el aislamiento de impactos.
El objetivo de este artículo es revisar los medios clásicos de control de impactos y proponer nuevas alternativas que hagan uso de la nueva generación de materiales y estructuras inteligentes.
FUNDAMENTOS
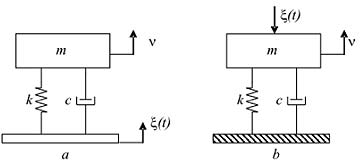
El modelo clásico que se ha usado para estudiar los efectos de impactos, cuantifi car el daño potencial y seleccionar aisladores es el bien conocido sistema de un grado de libertad masa-resorte-amortiguador (MKC), ilustrado en la fi gura 1. Existen dos enfoques dependiendo de si el sistema es excitado por la base, o si la excitación es aplicada directamente a la masa. En este trabajo se presta atención a sistemas excitados por la base, sin embargo, la ecuación característica tiene la misma forma en cualquiera de los dos casos por lo que los resultados son aplicables en ambas situaciones.
|
Fig. 1. Modelos de un grado de libertad usados para el análisis de vibración transitoria: (a) excitación por desplazamiento en la base, (b) excitación por fuerza aplicada en la masa. |
La ecuación característica del sistema presentado en la fi gura 1 está dada por (1):
|
|
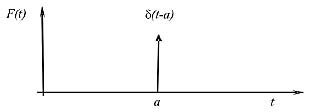
Uno de los principales problemas cuando se trata de estimar la respuesta de un sistema sujeto a impactos, es idealizar la excitación. En las simulaciones, aún y cuando en muchas ocasiones se usa información procedente de impactos reales, lo más común es manejar excitaciones por medio de funciones matemáticas. La manera más sencilla de simular un impacto es por medio de una versión escalada de la función delta de Dirac δ (t), representada en la fi gura 2, la cual es adecuada para impactos de muy corta duración y es simulada en sistemas mecánicos como un impulso, o cambio inmediato en la velocidad sin alteración en el desplazamiento inicial.
|
Fig. 2. Función delta de Dirac aplicada en el instante de tiempo a. |
Cuando los impactos son más complejos o de mayor duración, hay que considerar otras funciones para la forma del pulso. Muchas situaciones reales pueden simularse con un alto grado de exactitud usando este tipo de funciones, sin embargo es necesario tener un amplio conocimiento de la situación que se estudia, y las características de cada pulso, por ejemplo en cuanto a su contenido de frecuencias, para usar la función que más se adapte a la realidad.
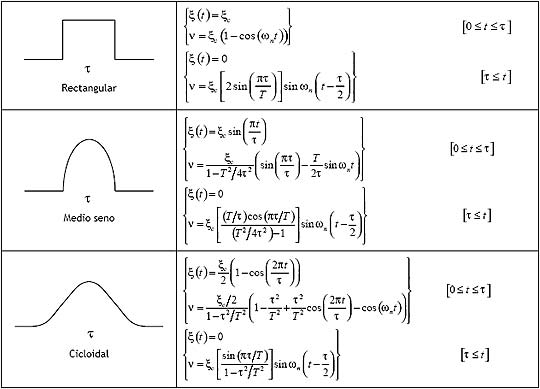
La tabla I ilustra la forma de pulsos, junto con sus expresiones matemáticas, para algunas de las excitaciones transitorias más comunes. En esta tabla c ξ representa la máxima amplitud del pulso y τ su duración.
|
Tabla I. Funciones de pulso comúnmente usadas en el análisis de sistemas bajo impactos. |
Otro punto importante es el hecho de que la excitación transitoria c ξ puede tomar diversas formas dependiendo de la situación, puediéndose presentar como una fuerza, un desplazamiento, aceleración o incluso un par torsor. Es por eso que en este artículo la respuesta del sistema y la excitación son consideradas genéricas dado que la ecuación característica presenta la misma forma.1 Además es importante indicar que los parámetros de respuesta más importantes para evaluar impactos y seleccionar aisladores, los cuales están relacionados,2 son:
- Los valores máximos de desplazamiento y aceleración absolutos (conocido como respuesta maximax: la máxima respuesta en cualquier instante).
- El valor máximo de desplazamiento relativo, que indica la deformación en el elemento elástico.
- La respuesta máxima una vez que el impacto ha terminado, conocida como respuesta residual.
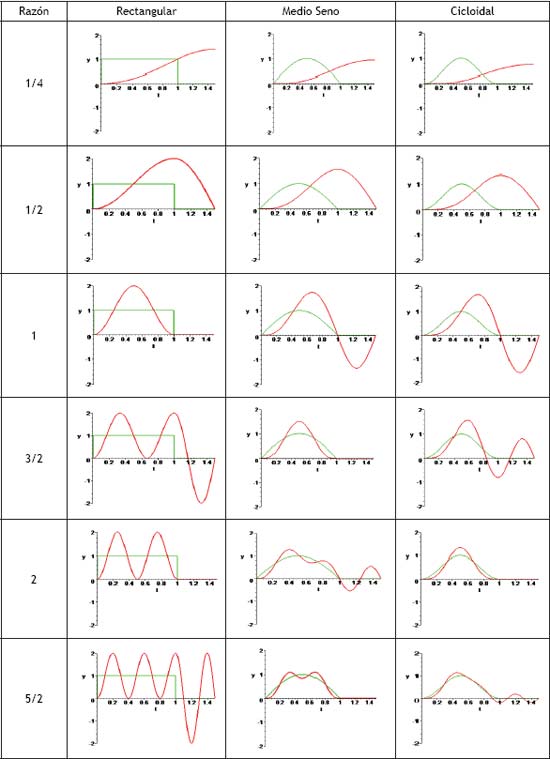
En la tabla II se ilustra una serie de respuestas típicas para tres pulsos simétricos, en función de la duración del pulso τ y el periodo natural del sistema T. La importancia del parámetro τ /T radica en que es un indicador de la duración del pulso tomando como referencia el periodo natural del sistema, y permite distinguir tres casos principales dependiendo del valor de τ /T:
- τ /T <0.25. En este caso el impacto es de corta duración comparado con el periodo natural del sistema. La respuesta máxima ocurrirá después de que el impacto ha sido aplicado y su amplitud es menor que la amplitud del impacto. La forma del impacto casi no tiene importancia. Es importante destacar que en el caso del pulso rectangular estas características se dan aproximadamente para valores de τ /T < 0.16 dado que este pulso es de una naturaleza distinta porque alcanza su amplitud máxima de manera inmediata.
- τ /T ≈1. La respuesta máxima ocurre mientras el impacto es aplicado, y su amplitud es mayor. Se dice que la respuesta se amplifica.
- τ /T >2. La duración del pulso es mucho mayor comparada con el periodo natural del sistema. A medida que τ /T aumenta la respuesta se aproxima al pulso, de manera que sus amplitudes son muy parecidas. Es por esto que la forma del pulso toma mayor importancia. El impacto se torna quasiestático.
|
Tabla II. Respuestas típicas de un sistema de un grado de libertad sin amortiguamiento sujeto a tres diferentes pulsos con distintas duraciones relativas al periodo natural del sistema. |
Para analizar con mayor facilidad impactos, se ha creado una herramienta muy útil, conocida como espectro de impacto4 (SRS, por sus siglas en inglés, Shock Response Spectra). A pesar de que el nombre espectro implica una gráfica en el dominio de la frecuencia, el SRS es más bien una gráfica en el dominio del tiempo, dado que representa la respuesta (que puede ser relativa, residual o máxima) para una serie de sistemas MKC con diferentes valores de periodo natural, sujetos a la acción de un impacto. La respuesta se grafica normalizada en función de la amplitud del pulso como / v ξ (el cual es un parámetro análogo a la transmisibilidad en el caso de vibración armónica), contra el parámetro adimensional τ /T y el resultado es el espectro de impacto.
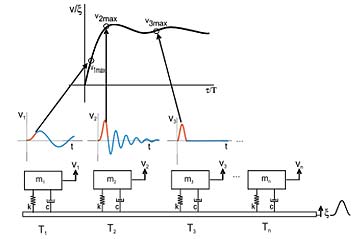
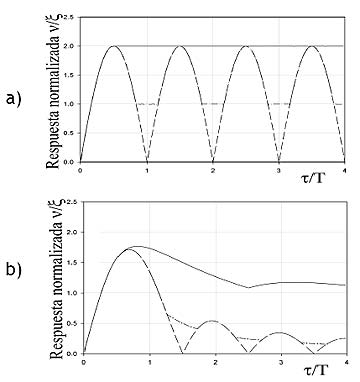
La figura 3 representa el concepto del SRS, donde la respuesta máxima de cada sistema se grafica para obtener el SRS, mientras que la figura 4 muestra espectros de impacto típicos para diferentes pulsos, en este caso para un sistema sin amortiguamiento.
AISLAMIENTO POR MEDIOS PASIVOS
El aislamiento es la acción de minimizar la transmisión de energía entre la máquina o sistema mecánico y su base. Esto se efectúa, en el diseño clásico, mediante un aislador, esto es, seleccionando la elasticidad y amortiguamiento de los elementos (conjunto k-c) que conectan la masa del sistema con el piso.
El espectro de impacto es usado tanto para evaluar la severidad de impactos en un sistema, como para la selección de aisladores adecuados. Para una mayor comprensión del uso del SRS en la selección de aisladores, se toma como ejemplo el caso de una excitación de tipo medio seno, el cual es uno de los pulsos más comúnmente usados. El SRS para este ejemplo se representa en la figura 5, en este caso considerado un sistema con amortiguamiento viscoso.
|
Fig. 3. Concepto del espectro de impacto por medio de una serie de sistemas MKC sujetos a un impacto.
Fig. 4. Espectro de impacto para los pulsos: (a) Rectangular, (b) Medio seno. |
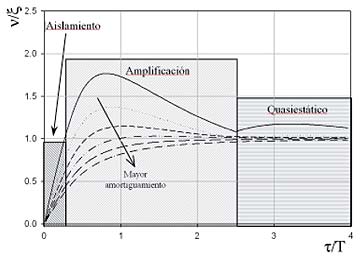
Se pueden observar en la figura 5 las tres zonas principales que existen en cualquier SRS, las cuales tienen las siguientes características:
- Zona de aislamiento.- Se caracteriza porque la amplitud de la respuesta máxima es menor a la amplitud del impacto, / v ξ , < 1. Esta zona representa una respuesta impulsiva, ya que el impacto es de corta duración (es decir, muy cercano a un impulso). Esta zona es conocida como región de aislamiento, dado que el aislador efectivamente minimiza la vibración transmitida.
- Zona de amplificación.- En la zona media se encuentran los impactos cuya duración es cercana al periodo natural del sistema, y en este caso la respuesta es amplifi cada. Es en esta zona donde al amortiguamiento tiene un mayor efecto en cuanto a reducir la respuesta del sistema.
- Zona quasiestática.- Por último la zona caracterizada por impactos de larga duración, o quasiestática, donde la respuesta tiende a coincidir con el pulso, y el amortiguamiento tiene un efecto mínimo.
|
Fig. 5. Espectro de impacto para un pulso medio seno, aplicado a sistemas amortiguados, explicando las tres regiones existentes: Zona de aislamiento, zona de amplifi cación y zona quasiestática. |
De lo anterior se deduce que para elegir un aislador adecuado, las propiedades de éste deberán ser tales que τ /T sea muy pequeño, lo cual se consigue diseñando el aislador de tal manera que su periodo natural T sea muy alto en comparación con la duración de los impactos τ a los que el sistema esté sometido, lo cual implica aisladores con una rigidez muy baja, para que de esta forma los elementos elásticos sean capaces de absorber la mayor parte de la energía proveniente del impacto. De hecho, será el elemento elástico el que absorberá la energía y no el elemento amortiguante.
Es claramente visible que sólo altos niveles de amortiguamiento pueden lograr reducciones considerables en la respuesta del sistema, pero investigaciones recientes han demostrado que un alto amortiguamiento tiende a elevar los niveles de aceleración en situaciones de impacto5 produciendo efectos indeseables, por lo que el principal elemento a considerar para aislar los impactos es la elasticidad. Sin embargo, el amortiguamiento es aún necesario para suprimir las vibraciones residuales y lograr que el sistema regrese al equilibrio en un tiempo mínimo.
En resumen, el aislador debe ser muy elástico. Sin embargo, esto no es siempre posible por dos razones. La primera es que el aislador debe ser lo sufi cientemente rígido como para soportar el peso estático del sistema a aislar. La segunda es que debido a la naturaleza de los elementos elásticos, para poder absorber energía deben de permitirse grandes deformaciones elásticas. Esto implica que el desplazamiento relativo entre la base y la masa a aislar es muy grande, para lo cual se requiere espacio disponible, y muchas veces el espacio es una restricción.6
AISLAMIENTO POR MEDIOS ACTIVOS/ SEMIACTIVOS
De la anterior sección se deduce que para obtener un aislador óptimo por el método tradicional hay un compromiso entre los diversos parámetros: Un soporte que durante el impacto sea lo sufi cientemente suave como para absorber grandes cantidades de energía, pero que pueda ser rígido en condiciones normales, y a la vez moderadamente amortiguado durante los impactos, pero con un nivel alto de amortiguamiento después del impacto para minimizar vibraciones residuales.
Un soporte de este tipo es imposible de obtener por medios pasivos. Sin embargo es posible conseguir estas cualidades con el uso de sistemas activos o semiactivos. Una de las primeras investigaciones que hizo notar este punto es la monografía hecha por Sevin y Pilkey7 donde se concluye que para que un aislador sea óptimo deberá ser activo.
Existen diversos esquemas de aislamiento/control activo de vibraciones, dependiendo de la naturaleza de los sistemas de control, los que se pueden clasificar en: completamente activos, semi activos y adaptativos.
Un sistema de control completamente activo de vibraciones es aquel que es capaz de introducir una fuerza de control Fc en contrafase a la fuerza de excitación por medio de actuadores8 para, al menos en teoría, suprimir la fuerza perturbadora y lograr en la práctica que el sistema se mantenga lo más cercano a su posición de equilibrio. Por medio de sensores que miden la respuesta y la excitación del sistema, un sistema de control, que puede ser digital o analógico, se encarga de establecer la magnitud y dirección de la fuerza de control Fc que derive en un aislamiento vibratorio óptimo.
Dichos sistemas pueden llegar a ser muy eficientes si son diseñados correctamente, pero tienen ciertas desventajas. La primera estriba en el hecho de que se requiere introducir energía al sistema, lo cual puede causar inestabilidades bajo ciertas condiciones, y además su costo se eleva por el alto consumo de energía y los complejos sistemas de control y tratamiento de señales invoclucrados. Otra desventaja es que si se presenta alguna falla no se dispone de un sistema de respaldo. Otros aspectos de suma importancia en este tipo de sistemas es la localización de los actuadores y sensores, así como la cantidad requerida de éstos.
Por otra parte, los sistemas semi-activos y adaptativos9 han sido desarrollados para compensar las desventajas existentes en sistemas completamente activos. En este tipo de controles, no se introduce energía al sistema, sino que las propiedades físicas del aislador: la elasticidad y el amortiguamiento, se adaptan a diversas situaciones para tratar de ofrecer siempre un rendimiento óptimo.
La diferencia entre un sistema semi-activo y uno adaptativo radica en que en el primer caso las propiedades, léase elasticidad o amortiguamiento, cambian en cada ciclo de vibración. Por ejemplo, con un control semi-activo de amortiguamiento variable sujeto a una excitación armónica de cierta frecuencia, el amortiguamiento estará cambiando de acuerdo a la frecuencia de excitación. Es por eso que este tipo de sistemas se aplican principalmente a excitaciones periódicas. Por otro lado, en un sistema adaptativo, la variación en los parámetros del sistema es tal que éstos se adaptan más lentamente a ciertas situaciones, por ejemplo la suspensión de un automóvil, que puede ajustar sus propiedades dependiendo del tipo de camino.
Como resultado, en ambas configuraciones se consume menos energía y no hay riesgo de inestabilidad, además si existe un fallo en el sistema, en el peor de los casos ofrecerá el rendimiento de un sistema pasivo, lo cual no sucede en el esquema completamente activo.
|
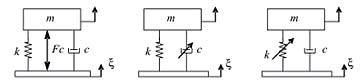
Fig. 6. Estrategias de control de vibraciones: (a) Control completamente activo, (b) Control adaptativo de amortiguamiento variable, (c) Control adaptativo de elasticidad variable. |
La figura 6 ilustra los diversos tipos de control activo y semi-activo/adaptativo.
Para conseguir la variación de los parámetros elasticidad y amortiguamiento en sistemas semiactivos y adaptativos en la práctica, existen diversos métodos. Dentro de la categoría de sistemas de amortiguamiento variable, los primeros dispositivos consistieron en amortiguadores de fluido con orificios variables, de esta manera al regular el flujo se consigue un cambio en la constante de amortiguamiento. Actualmente los medios más usados para conseguir amortiguadores variables, son los fluidos electroreológicos y magnetoreológicos, los cuales son capaces de incrementar su amortiguamiento
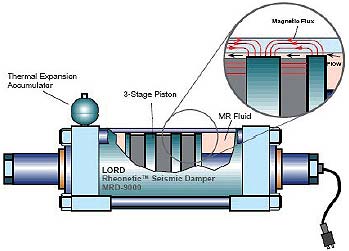
ante la presencia de un campo eléctrico o magnético, dependiendo del caso. Sus principales ventajas son una rápida velocidad de reacción, en el orden de los milisegundos, pero como desventajas se tienen los altos voltajes requeridos, y el comportamiento no lineal que presentan.11 En la figura 7 se muestra un esquema de un amortiguador variable disponible comercialmente.
Por otro lado, en el caso de elasticidad variable existen diversos dispositivos. De los más comunes son los materiales piezoeléctricos, que tienen la propiedad de generar un voltaje cuando son sometidos a esfuerzos mecánicos, los cuales también son capaces de experimentar el efecto contrario, es decir, presentar deformaciones al ser sometidos a un voltaje. De esta manera pueden ser usados como sensores y/o actuadores. Al ser usados como actuadores, pueden “endurecer” un sistema al ser usados en forma de parches. Tienen una velocidad de respuesta muy alta, pero el rango de uso es limitado y además son normalmente frágiles.
|
Fig. 7. Diagrama de amortiguador variable de tipo magnetoreológico, marca Lord. |
Otros materiales de propiedades semejantes son los llamados electrostrictivos y magnetostrictivos, los cuales reaccionan ante la presencia de campos eléctricos o magnéticos respectivamente, provocando deformaciones. Comparados con los piezoeléctricos tienen una mayor capacidad, en términos de fuerza, sin embargo son más sensibles a los cambios de temperatura, y en el caso de los magnetostrictivos, sólo pueden ser usados en compresión.
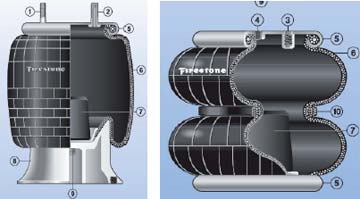
También existen las aleaciones con memoria de forma, las cuales como su nombre indica, pueden recobrar una forma preestablecida cuando se les somete a un cambio de temperatura. Son capaces de inducir grandes fuerzas debido a las altas deformaciones involucradas, sin embargo su tiempo de reacción es muy elevado. Existen además medios mecánicos, como la variación del número de espiras en resortes helicoidales, resortes de hoja variables, sistemas de conexión-reconexión de resortes por mecanismos de fricción, y los resortes de aire, ver figura 8, entre otros.12
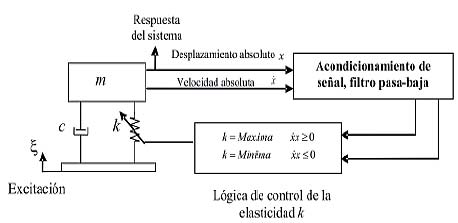
La figura 9 ilustra un ejemplo de esquema de control de un sistema con elasticidad variable. En este caso las variables usadas son la velocidad y el desplazamiento absolutos y el producto de estas variables defi ne el valor de la elasticidad a usar. Esta lógica es usada en sistemas con poco amortiguamiento, con el fin de atenuar las vibraciones modificando la rigidez de los elementos elásticos.
|
Fig. 8. Ejemplos de elementos elásticos variables de aire disponibles comercialmente, marca Firestone.
Fig. 9. Ejemplo de lógica de elasticidad variable. |
El uso de sistemas de control ha sido muy común durante los últimos años y hay una gran cantidad de estudios relativos a excitación armónica y aleatoria, sin embargo en lo referente a impactos la literatura disponible es considerablemente menor. Algunas excepciones notables son los trabajos de Balandin, et al.13,14 quienes han estudiado el diseño de aisladoresóptimos, por medios activos y pasivos, y ha llegado a la conclusión de que se pueden obtener grandes mejoras al implemetar sistemas de control predictivo de tal manera que actúen antes de la perturbación, pero para esto se requiere contar con información previa al impacto lo cual no siempre es posible o fácil de realizar. En el caso de sistemas completamente activos las investigaciones se reducen aún más debido a la complejidad de dichos sistemas.15
El caso de amortiguamiento variable es uno de los que ha sido estudiado más a fondo.16 Recientemente diversas estrategias de amortiguamiento variable17 han sido sometidas a evaluación por medio de simulaciones en diversas situaciones de impacto, variandose el amortiguamiento entre un valor mínimo y un máximo dependiendo de una lógica de control, sin embargo se ha llegado a la conclusión de que al menos en el caso de impactos no se obtienen ventajas al usar estas estrategias.16,17
Como ejemplo de lo antes mencionado en la figura 10 se muestra una comparación entre un sistema pasivo y uno al que se le aplican diferentes estrategias de control de amortiguamiento variable. Es claro que el pico de la respuesta vibratoria cuando se utiliza amortiguamiento variable es siempre mayor que la del sistema pasivo, teniendo ambos sistemas el mismo amortiguamiento máximo.
Debido a la ineficacia de los sistemas de amortiguamiento variable para atacar exitosamente los problemas de impacto, la estrategia que luce más prometedora es el uso de sistemas de elasticidad variable. De esta manera el sistema puede adaptar su elasticidad (es decir, volverse más “suave”) durante la aplicación de un impacto y después volver a su estado inicial. Existen pocas investigaciones de este tipo de sistemas18 y la mayor parte de los estudios de elasticidad variable se centran en la supresión de vibraciones residuales como una alternativa al amortiguamiento en sistemas y estructuras ligeras19 y dispositivos absorbentes de vibración adaptativos.20
|
Fig. 10. Respuesta de un sistema MKC bajo el efecto de un pulso cicloidal para diversas estrategias de amortiguamiento variable: (a) τ /T = 0.25 (b)τ /T =1. |
Existen ciertas consideraciones y limitaciones a tomar en cuenta para la implementación de un sistema de elasticidad variable. La principal es la capacidad de los sistemas actuales para lograr una variación considerable en la elasticidad en un tiempo mínimo. Para poder garantizar una reducción efectiva en la respuesta de impacto se necesita una reducción de la rigidez en un 80% al menos. Muchos de los materiales inteligentes como los parches piezoeléctricos tienen un tiempo de reacción bastante corto, pero su capacidad de cambiar la elasticidad no es muy alta.
Por el contrario, con medios mecánicos se pueden obtener grandes porcentajes de cambio en la elasticidad, pero en un tiempo relativamente elevado. Acualmente los estudios se dedican a la evaluación de diversos medios por los cuales podrá ser posible la implementación de mejores actuadores. Sin embargo, una vez superados estos problemas se podrá obtener un sistema de aislamiento de impactos de alta eficacia.
La idea fundamental de dicho sistema implica establecer un sistema de aislamiento por etapas, siendo la primera etapa la reducción de la respuesta máxima aumentando la elasticidad y con muy poco o nulo amortiguamiento durante el impacto para absorber la mayor cantidad de energía proveniente del impacto, y posteriormente minimizar la vibración residual, ya sea aumentando la cantidad de amortiguamiento, o estableciendo una estrategia alterna para la atenuación de estas vibraciones.
Otro punto importante a considerar es el buscar contar con información de previsualización que permita anticipar un impacto e iniciar un control por etapas a tiempo.
CONCLUSIONES
La importancia de los sistemas de aislamiento de impacto ha sido discutida y analizada, así como los fundamentos de la teoría de análisis y control de impactos basado en el espectro de impacto. Se ha establecido que el parámetro más importante en el control de la respuesta máxima de un sistema es la elasticidad, mientras que el amortiguamiento sólo es útil en la zona de amplifi cación del espectro de impacto, donde su efecto es más considerable, y también es necesario para suprimir las vibraciones residuales después del impacto.
Las posibilidades y estudios previos acerca de control activo y semiactivo de impactos han sido comentadas y un punto importante a mencionar es la necesidad de más investigaciones en el tema. Particularmente se ha puesto atención al control de impactos por medio de estrategias de amortiguamiento variables, pero estas estrategias no ofrecen ventajas en el caso de impactos.
Por otro lado las estrategias de variación de la elasticidad para el control de impactos se presentan con muchas posibilidades de éxito, por supuesto que una vez que sea superado el problema de conseguir un dispositivo que pueda proveer una gran reducción de la rigidez en tiempos muy cortos.
Se vislumbra la necesidad de una estrategia de control que no esté limitada a una sola variable, sino a varias, en este caso al menos la elasticidad y el amortiguamiento, y a considerar el control del impacto en etapas. El control de la elasticidad durante la primera etapa estará enfocado a minimizar la respuesta pico durante la aplicación de un impacto y posteriormente esta misma etapa servirá para disparar la segunda cuyo objetivo es minimizar las vibraciones residuales restituyendo la elasticidad original y aumentando el amortiguamiento.
REFERENCIAS
- Harris, C.M., Creede, C.E., Shock and vibration handbook, McGraw-Hill, New York,1996.
- Lalanne, C., Mechanical vibration and shock, volume 2, Mechanical shock, Hermes science publications, Paris 2002.
- Ayre,R.S., Engineering vibrations, McGraw-Hill, New York,1958.
- Irvine,T. An Introduction to the shock response spectra, http://www.vibrationdata.com/tutorials2/ srs_intr.pdf, 2002.
- Miindlin, R. D., Dynamics of package cushioning, Bell System Technical Journal, 24 353-467 1945.
- Mercer, C.A., Rees, P.C., An optimum shock isolator, Journal of Sound and Vibration, 1971, 18(4), 511-20.
- Sevin, E., Pilkey, W.D., Optimum shock and vibration isolation, the shock and vibration information center, United States Department of Defense, 1971.
- Brenan, M.J., Garcia-Bonito, J., Elliot, S.J., Pinnington R., Experimental investigation of diferent actuator techologies for active vibration control, smart materials and structures, 1999, 8, 145-153.
- Jalili, N., A comparative study and analysis of semi active vibration control systems, Journal of vibration and acoustics, Octubre 2002, 124, 593-605.
- Crosby, M.J., Karnopp, D.C., The active damper: a new concept for shock and vibration control, shock and vibration bulletin, 1973, 43 119- 133.
- Schwartz, M,. Encyclopaedia of smart materials, John Wiley and Sons, New York,2002.
- Winthrop,. M.F., Baker, W.P., Cobb, R.GA Variable stiffness device selection and a design tool for lightly damped structures. Journal of sound and vibration, 2005, 287(1), 667-82.
- Balandin, D.V., Bolotnik, N.N., Review: Optimal shock and vibration isolation. Shock And vibration, 1998, 5 73-87.
- Balandin, D.V., Bolotnik, N.N., Pre-acting control for shock and impact. Shock and vibration, 2005, 12 49-63.
- Tanaka, N., Kikushima, J., Active control of impact vibration using feedforward control method, Journal of vibrations, acoustics and reliability in design, enero 1989, 11, 53-61.
- Liu, Y., Waters, T.P., and Brennan, M.J., A comparison of semi active damping control strategies for vibration isolation of harmonic disturbances. Journal of Sound and Vibration, 2005, 280, 21-39.
- Ledezma, D.F., Ferguson, N.S., Brenan, M.J., shock isolation of a single degree of freedom system, recent advances in structural dynamics conference, 2006.
- Krishna, Y., Sarma, B.S., Shirivanasa, U., Shock isolation using magnetostrictive actuator, smart structures and materials, Proceedings of SPIE, 2003, 5062 270-77.
- Onoda, J., Watanabe, N., Vibration suppression by Variable Stiffness Members, AIAA Journal, June 1991, 29(6), 977-83.
- Holdhusen, M., Cunefare, K.A., Investigation of the two state, Maximum work extraction switching rule of a State-Switched absorber for vibration control. Active 04 2004.
Por: Diego Francisco Ledezma; Ramírez, Neil Ferguson
Institute of Sound and Vibration Research, University of Southampton
dfl @isvr.soton.ac.uk, [email protected]
Fernando Javier Elizondo Garza
Laboratorio de Acústica, FIME-UANL [email protected]
Fuente: ingenierias.uanl.mx
Vea también nuestros contenidos
de SEGURIDAD EN LA CONSTRUCCIÓN