Modelos de optimización para el diseño sostenible de cadenas de suministros de reciclaje de múltiples productos

RESUMEN:

Este trabajo presenta un modelo multiobjetivo no lineal entero mixto (MINLP) para el diseño sostenible de cadenas de suministro para el reciclaje de varios materiales. En él se integran objetivos económicos y medioambientales para soportar la toma de decisiones estratégicas y tácticas tales como la localización de instalaciones, el diseño de los flujos materiales y la selección de medios de transporte. La evaluación del impacto medioambiental se realiza a través de la metodología de Análisis del Ciclo de Vida (LCA) utilizando el Ecoindicador 99. Se modeló un caso de estudio para la cadena de reciclaje de dos tipos de plástico, utilizando el método de las restricciones para obtener la frontera de Pareto. En el desarrollo del caso se mostraron indicadores que permiten evaluar las soluciones encontradas y así facilitar el proceso de toma de decisiones.

Palabras clave: diseño de la cadena de suministros, logística inversa, modelo de optimización, sostenibilidad.

INTRODUCCIÓN

El Desarrollo Sostenible es el desarrollo que satisface las necesidades de la generación presente sin comprometer la capacidad de las generaciones futuras para satisfacer sus propias necesidades [1]. Este término fue presentado en 1987 por la Comisión Mundial de Medioambiente y Desarrollo en el reporte de Brundtland. La búsqueda del desarrollo sostenible ha creado una nueva disciplina científica, llamada Ciencia de la Sostenibilidad, con problemas que no pueden enfrentarse con las herramientas metodológicas de las disciplinas científicas clásicas [2-6]. Esta disciplina explora las relaciones e interacciones de la actividad humana con los ecosistemas que soportan la vida para encontrar un camino hacia un desarrollo humano sostenible.

La mayoría de los intentos de conceptualización de la sostenibilidad en el contexto microeconómico se enfocaron en la sostenibilidad medioambiental [7], con un reconocimiento social y económico implícito. La sostenibilidad de las organizaciones socioeconómicas en un nivel agregado depende fundamentalmente de tres dimensiones: la ambiental, la social y la económica [8-9]. Esta perspectiva está basada en la idea de los tres pilares de la sostenibilidad desarrollada por Elkington [10] el cual considera que deben ser balanceadas para que las organizaciones sean sostenibles. El concepto de Gestión de la Cadena de Suministros Sostenible (GCSS) está derivado del concepto de Gestión de la Cadena de Suministros.

Seuring y Müller [11] definen la GCSS como la gestión de materiales, información y flujos de capital así como la cooperación entre las compañías a lo largo de la cadena, teniendo en cuenta las metas de las tres dimensiones del desarrollo sostenible, ecológicas, económicas y sociales, derivadas de los requerimientos de los consumidores y los grupos de interés. Carter y Rogers [8] consideran que la GCSS se enfoca en metas a largo plazo económicas, ecológicas y sociales para mejorar el desempeño económico y competitivo de las organizaciones que participan en la cadena.

Una de las prácticas empresariales asociadas a la sostenibilidad de las cadenas de suministros es sin duda la llamada logística inversa, la cual se puede describir como el conjunto de actividades de gestión, que se ocupa de devolver los productos y materiales a los procesos productivos y mercados, para lograr ventajas competitivas, revalorización de estos materiales y reducir el impacto de estos productos en la naturaleza.

La logística inversa tiene varios problemas propios, diferentes de la logística directa [12- 13] y cada vez más constituye un motivo de interés científico y práctico para la ciencia de las cadenas de suministro y la logística. Se resalta el poco carácter estratégico de las prácticas de la logística inversa, así como otros problemas que todavía son motivos de investigación: la integración con la logística directa desde el diseño no solo de las redes logísticas sino de los productos y las tecnologías; el manejo de la incertidumbre en la cantidad y la calidad de los productos y materiales recuperados, así como en la demanda, precios y la generación de los mismos; la inclusión de estos procesos en las decisiones del ciclo de vida de los productos; y la medición de los impactos ambientales, económicos y sociales derivados de los procesos de la logística inversa y su utilización en los modelos cuantitativos para apoyar la toma de decisiones.

Existen empresas que se dedican a la tercerización de la logística inversa para las cadenas de suministros. Comúnmente se especializan en algún tipo específico de producto, aunque algunas comparten sus recursos e instalaciones en múltiples productos y residuos reciclables [14]. En los últimos años se ha producido un incremento en la generación de residuos y desechos: productos devueltos, ociosos, el cambio de equipos por tecnologías más novedosas en la industria, así mismo se incorporan cada vez más productos, partes o materiales recuperados de vuelta
a los procesos productivos y mercados, por lo que cada vez más se necesita de empresas y cadenas que desempeñen esta labor eficientemente [15].

Es importante el desarrollo y uso de herramientas matemáticas que permitan diseñar la cadena de suministros dedicadas a la recuperación de múltiples materiales reciclables. La recuperación de diferentes productos que comparten instalaciones y medios de transporte, unido a las condiciones de incertidumbre tanto en la generación como en la demanda, constituyen un reto para el diseño y gestión de la cadena de suministros. El compromiso de brindar materiales reciclados que aporten al desarrollo sostenible, provoca la necesidad de cumplir con objetivos económicos, sociales y ecológicos en estos diseños.

Diseño de las Cadenas de Suministros Sostenibles Un elemento esencial en la GCSS es lograr un diseño de la cadena que permita un desempeño sostenible de la misma. Ello involucra aspectos tanto estratégicos como tácticos y relaciona varias áreas importantes de la logística (localización, capacidad, flujos y transporte) que, en la práctica más común, se gestionan de manera independiente realizando esfuerzos en óptimos locales y no en la optimización del sistema. Esta decisión, costosa en tiempo y dinero, comprende la determinación del número, capacidad y localización de las instalaciones necesarias y el diseño de los flujos de materiales para satisfacer a los clientes de manera eficiente.

Las cadenas de suministros se encuentran cada vez más presionadas por diversos grupos de interés a tomar decisiones no sólo basadas en objetivos económicos, sino que se deben incluir objetivos ambientales y sociales [9].

Cada vez más se hace hincapié en la relación de las cadenas de suministro con el medioambiente. La gestión de la cadena de suministro inversa o de ciclo cerrado (directa más inversa) ha sido objeto de estudio importante desde hace aproximadamente una veintena de años y aunque es todavía un área de investigación novedosa, varios autores han propuesto modelos cuantitativos para soportar la toma de diferentes decisiones como: diseño de productos y selección de productos utilizados [16-19], decisiones sobre centros de recolección e instalaciones de recuperación [20-22] y optimización del transporte [23-25].

Varios autores reconocen la importancia de la logística inversa en el diseño de las cadenas de suministros [26-29] y sus aportes indiscutibles para la mejora del desempeño ambiental de las organizaciones[30]. Las investigaciones actuales están cada vez más enfocadas hacia el cuidado del medioambiente para lograr una empresa sostenible y por tanto más competitiva [8, 31].

El diseño de la cadena de suministros utilizando conjuntamente objetivos económicos y medioambientales ha sido tratada por Frota Neto, Bloemhof-Ruwaard, Van Nunen y Van Heck [28] en un modelo para la asignación de los flujos de productos retornados en la cadena de papel. Chaabane, Ramudhin y Paquet [27] desarrollaron un modelo para un escenario de intercambio con bonos de carbono y Kannan, Diabat, Alrefaei, Govindan y Yong [32] utilizan la huella de carbono y el cambio climático como medida ambiental. Dehghanian y Mansour [33] también aportaron a través de un modelo utilizando el Análisis del Ciclo de Vida (LCA) y algoritmos genéticos para diseñar la cadena para la recuperación de neumáticos.

La cantidad de publicaciones y trabajos relacionados con modelos cuantitativos para el diseño de la cadena de suministros demuestra la actualidad y las posibilidades para abarcar el tema desde diferentes aristas. Los esfuerzos de integrar la dimensión medioambiental a la económica es todavía un tema vigente y novedoso. Dentro de las metodologías para la evaluación ambiental, el análisis del LCA ha sido una de las más exitosas y utilizadas desde la inclusión en las normas internacionales ISO 14040 e ISO 14044 para su aplicación. Sus posibilidades para la integración con otras metodologías relacionadas con la toma de decisiones son motivadoras para presentes y futuras investigaciones [27, 29] en el diseño de las cadenas de suministros.

En todos los casos revisados se modela la cadena para un solo producto, utilizan los impactos ambientales fundamentalmente medidos en emisiones de CO2, por producir, por reciclar, por incinerar y por transportar. Los resultados de esas funciones objetivo solamente pueden medir el impacto ambiental en función de los flujos de materiales producidos, reciclados o desperdiciados pero no describen cómo el número de instalaciones o su localización puede afectar el impacto sobre el medioambiente. Las decisiones que se toman son de localización y capacidad de instalaciones a partir de la optimización de los flujos, dejando fuera otras posibles decisiones tácticas como la asignación de viajes y selección de la capacidad de los medios de transporte. Los modelos revisados [27, 28, 32, 33] no pueden ser adaptados a las condiciones de una cadena de recuperación de múltiples productos por lo que esta investigación tiene como objetivo construir un modelo de programación no lineal entera mixto (MINLP) que conjugue objetivos económicos y ambientales con el fin de obtener un diseño de la cadena de suministros para la recuperación de múltiples productos que facilite una gestión sostenible del reciclaje.

Para facilitar el cumplimiento de este objetivo, el trabajo se estructura de la siguiente manera: primeramente se realiza una descripción del modelo propuesto para el diseño de una cadena de suministro sostenible de reciclaje de múltiples productos. Ello incluye, el planeamiento de los supuestos del modelo, los parámetros, funciones objetivo, restricciones, así como el procedimiento para su operación. Seguidamente se aborda la aplicación del modelo a través de un caso de estudio para diseñar una cadena de suministros de reciclaje de plásticos y finalmente se presentan las conclusiones de la investigación.

ESTRUCTURA DEL MODELO

Modelo multiobjetivo no lineal para el diseño de cadenas de suministro de reciclaje de múltiples productos
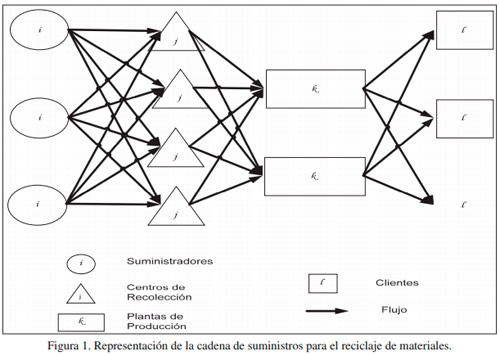
El diseño de la cadena de suministro para el reciclaje consiste en determinar los centros de recolección y las plantas de procesamiento, así como las necesidades de transporte que permita cumplir con la demanda optimizando los costos de operaciones y la utilización de las capacidades. Los elementos de esta red se muestran en la Figura 1.

La generación de los residuos en las fuentes tiene un comportamiento estocástico, de ahí se transportan a los centros de recolección, y de ahí a las plantas de procesamiento desde donde se distribuye a los clientes, cuya demanda tiene también un comportamiento estocástico. El modelo para resolver este problema tiene las siguientes asunciones:

1. El modelo contempla varios residuos.
2. La localización de los suministradores y clientes es conocida.
3. La posible localización de los centros de recolección y de las plantas de procesamiento es conocida.
4. Las capacidades de los centros de recolección son infinitas. (el objetivo es conocer cuál es la carga)
5. Las capacidades de las plantas de producción son finitas y conocidas.
6. Las cantidades de centros de distribución y plantas de producción son restringidas
7. La generación de los residuos y la demanda de las materias primas recuperadas tienen comportamiento estocástico.
8. La cantidad y capacidad de los medios de transporte potenciales son conocidas.
9. Los flujos solamente son permitidos entre dos eslabones consecutivos de la cadena y no se permiten flujos entre elementos del mismo eslabón, ni saltarse eslabones.

Los costos fijos y variables de producción, transportación y de los centros recolectores son conocidos y su comportamiento es determinístico.

La formalización del problema se puede expresar como sigue:

La formulación del modelo se muestra a continuación

Conjuntos

I: Conjunto de locales de proveedores generadores de residuos reciclables (i=1,2,…, I).
J: Conjunto de locales potenciales de centros de recolección (j=1,2,…, J).
K: Conjunto de plantas de procesamiento potenciales (k=1,2,…, K).
L: Conjunto de clientes (l=1,2,…, L).
M: Conjunto de medios de transporte potenciales (m=1,2,…, M).
P: Conjunto de productos a reciclar (p=1,2,…, P).

Variables de decisión

QSR_ijmp: Cantidad de producto p entre proveedor i y el centro de recolección j transportados en el medio m.
QRP_jkmp: Cantidad de producto p entre el centro de recolección j y la planta k transportados en el medio m.
QPC_klmp: Cantidad de producto p entre la planta k y el cliente l transportados en el medio m.
VSR_ijm: Cantidad de viajes entre el suministrador i y el centro de recolección j transportados en el medio m.
VRP_jkm: Cantidad de viajes entre el centro de recolección j y la planta k transportados en el camión m.
VPC_klm: Cantidad de viajes entre la planta de producción k y el cliente l transportados en el camión m.
HSR_ijm, HRP_jkm, HPC_klm, son variables para representar las cantidades por exceso y defecto producto de la diferencia entre la capacidad de los medios de transporte y las cantidades a transportar entre dos niveles.
R_j: 1 Si el centro de recolección j es utilizado, 0 si no es utilizado.
P_k: 1 Si la planta k es utilizada, 0 si no lo es.

Parámetros

G_ip: Cantidad de producto p del suministrador i generado en el período.
C_Tmp: Capacidad del transporte m para transportar el producto p.
C_kp: Capacidad de la planta k para procesar el producto p.
D_lp: Demanda de cada cliente l del producto p.
Nv_m: Cantidad de viajes disponibles en el período para cada medio de transporte m.

Parámetros utilizados para las funciones objetivo

I_p: Impacto ecológico por producir una unidad nueva del producto p.
IT: Impacto ecológico por transportar una tonelada kilómetro.
IE: Impacto ecológico por consumir un kilowatt hora en el sistema.
IP: Impacto ecológico por utilizar una planta de reciclaje.
IA: Impacto ecológico por consumir un kg de agua en el sistema.
IV_p: Impacto ecológico por desechar en un vertedero una unidad del producto p luego de su consumo.
Todos los impactos se determinan a través de LCA ya realizados y publicados en las bases de datos Ecoinvent.
Cfe_k: Consumo fijo eléctrico de la planta de reciclaje k (depende de los equipos consumidores eléctricos que no son directos a la producción necesarios para operar la planta).
Cfe_j : Consumo fijo eléctrico del centro recolector j.
Cve_p: Consumo variable de electricidad necesaria para procesar una unidad del producto p.
Cva_p: Consumo variable de agua necesaria para procesar una unidad del producto p.
α y β: Proporción de la capacidad de la planta de reciclaje k y centro recolector j respectivamente, de la planta de reciclaje tipo utilizada en la base de datos Ecoinvent.
d _RP^jk : Distancias entre el suministrador i y cada centro de recolección j.
d ^SR _ij : Distancias entre el centro de recolección j y cada planta de procesamiento k.
d ^PC_kl : Distancias entre la planta k y cada cliente l.

Costos

CUR_jp: Costo unitario del producto p en el centro de recolección j en $/Unidad.
CUP_kp: Costo unitario del producto p en la planta k en $/Unidad.
CUT_m: Costo variable por km del medio de transporte m en $/km.
CFR_j : Costo fijo por utilizar el centro de recolección j en $/período.
CFR_k: Costo fijo por utilizar la planta k en $/período.
CFT_m: Costo fijo por utilizar el medio de transporte m en un viaje en $/viaje.

Funciones objetivo

El modelo propuesto tiene tres objetivos fundamentales la satisfacción del cliente, la reducción de los costos de operación y la reducción del impacto ambiental del sistema, los cuales están representados por las ecuaciones (1)-(3). La función objetivo representada por la expresión 1 resume el costo de operación del sistema. El uso del LCA en la ecuación (2) describe el impacto ambiental. La función objetivo mostrada en la ecuación (3) describe el servicio al cliente. En este trabajo se toman los proveedores de materiales reciclables también como clientes de la cadena, a los cuales se les brinda el servicio de recuperar sus desechos.

La función objetivo representada en la ecuación (1) describe los costos de operación del sistema en un período determinado descritos a través del compromiso existente entre la necesidad de abrir y operar plantas de producción y centros de recolección y las necesidades de transportación entre los diferentes eslabones de la cadena. Este tipo de objetivos ya sea en función del costo o de los ingresos son explicados en la mayoría de los modelos para el diseño de la
cadena de suministros. Los costos de transportación cuentan con los costos fijos por viajes y los costos variables por kilómetro recorrido de cada medio de transporte. Los costos de producción de las plantas y de los centros de recolección también se encuentran separados en fijos por cada planta procesadora y variables por cada unidad de material procesado, esta ecuación está en función básicamente de los flujos de materiales reciclados, transportados y vendidos.

En esta función no se tienen en cuenta los costos de instalación y construcción de las plantas y locales, aunque en los análisis de factibilidad si se deberán considerar.

En esta investigación se disecciona la función objetivo para el impacto ambiental del reciclaje en sus fases del ciclo de vida según el árbol de procesos. A diferencia de las ecuaciones utilizadas en la literatura consultada, en esta función objetivo se evalúan mejor los compromisos entre la apertura de las instalaciones, las distancias entre ellas para la transportación, la energía consumida y el impacto del consumo de otros recursos utilizados en los procesos de recuperación para buscar las configuraciones de la cadena con mejor desempeño ambiental.

La ecuación (2) consta de tres partes fundamentales y describe el impacto ambiental evitado por la sustitución del producto nuevo por el reciclado. La primera sección representa el impacto ambiental generado durante el ciclo de vida de los materiales multiplicado por las cantidades que el sistema logístico puede reciclar y vender a sus clientes, por lo que constituye el impacto ambiental evitado por no utilizar un material nuevo.

La segunda parte de la ecuación representa el impacto ambiental generado por el sistema para recuperar las cantidades que serán sustituidas, fundamentalmente representadas por los consumos de energía y agua, el uso del transporte y la construcción y utilización de las instalaciones. Estos impactos están estrechamente ligados a las cantidades a recuperar y a las decisiones de localización y capacidad de las instalaciones.

En la tercera parte se agrega el impacto ambiental evitado por no desechar las cantidades recuperadas de estos materiales.

En relación con las funciones objetivo revisadas en la literatura [27-28, 33] la función propuesta se diferencia en que describe mejor las relaciones de compromiso entre el impacto ambiental de las instalaciones y el uso del transporte. La misma contempla no solo el impacto ambiental emitido por la cadena sino también se compara con el impacto evitado por utilizar materiales reciclables y por no desecharlos a la naturaleza. Es capaz de evaluar el impacto ambiental de diferentes materiales en la misma función, lo cual caracteriza mejor a las organizaciones que utilizan los mismos recursos para reciclar varias materias primas.

La tercera función objetivo es maximizar los flujos hacia los clientes, por lo que tiene estrecha relación con el Nivel de Servicio al Cliente.

Las ecuaciones (12)-(14) son necesarias para que las variables de holgura solo se encarguen de las diferencias entre los números de viajes, las cuales constituyen variables enteras y el balance de carga y capacidad de los medios de transporte descritas en las ecuaciones (9)-(11). Esto es necesario porque como las variables de holgura no se encuentran en las funciones objetivos el modelo puede decidir cargarle todo el valor en lugar de complementar la parte no entera por exceso o defecto. La restricción (15) limita el número de viajes por medio de transporte, donde Nvm es la cantidad máxima finita de viajes que puede dar el camión m en el período. Esta cantidad está determinada en función de los mantenimientos preventivos y la disponibilidad de fondo de tiempo del medio y del conductor. Las ecuaciones (16) y (17) constituyen ecuaciones no lineales que fuerzan a las variables binarias a adquirir el valor de 1 cuando existe flujo a través de algún centro recolector o planta de producción.

Al final del modelo es necesario establecer los límites de las variables: todas las variables que representan flujos son continuas y mayores o iguales que 0, las variables que representan el número de viajes entre un punto y otro son enteras también mayores o iguales a 0, las variables que constituyen las holguras son continuas mayores que -1 y menores que 1 y las variables binarias son enteras mayor o igual a 0 y menor o igual que 1.

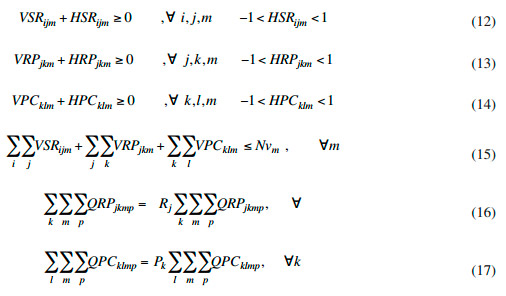
Solución del Modelo

Los problemas multiobjetivo no tienen una solución única óptima sino un conjunto de soluciones eficientes. Un vector solución x* se considera eficiente cuando no existe otro vector x que haga mejorar alguno de los objetivos, respecto a los valores obtenidos para x* sin que empeore de forma simultánea alguno de los otros. En general, la solución en el sentido de Pareto al problema de optimización multiobjetivo no será única: la solución estará formada por el conjunto de todos los vectores no dominados, a los que se conoce con el nombre de “frontera de Pareto”.

Existen varias estrategias para determinar soluciones a problemas con múltiples objetivos, uno de los métodos más utilizados es el de las restricciones el cual consiste en optimizar una función objetivo convirtiendo las otras en restricciones con parámetros variables en lado derecho.

La estrategia para construir el conjunto de soluciones Pareto-óptimas para este problema en particular se puede describir como:

3. Resolver el modelo descrito en la ecuación (18) y encontrar la solución correspondiente.
4. Repetir 2 y 3 hasta que se haya obtenido el conjunto de soluciones que pertenecen a la frontera de Pareto
5. Analizar las soluciones y seleccionar una configuración de la cadena de suministros

Desde esta perspectiva se brindan un conjunto de indicadores formados por relaciones entre los valores de las funciones objetivos para suministrar información adicional al centro encargado de tomar la decisión.

Caso de estudio: cadena de reciclaje de plásticos ERMP

Para demostrar la aplicabilidad del modelo se aplica al diseño de la cadena de suministros para la recolección de dos tipos de plásticos: los Polietilenos Tereftalatos (PET), fundamentalmente en forma de envases utilizados para aguas, refrescos y aceites, aunque también en forma de desecho industrial de las plantas de soplado de estos envases; y los Polietilenos (PEL) de alta y baja densidad de diversas formas.

Los elementos de la cadena de suministros presentes en el modelo son: 3 suministradores, 5 posibles centros de recolección, 2 posibles plantas de producción, 4 clientes y 2 grupos de medios de transporte: de mediano porte de hasta 16 toneladas y de gran porte de hasta 28 toneladas.

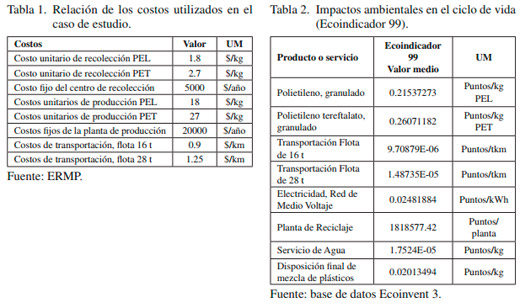
Actualmente estos productos se reciclan a través de la Empresa de Recuperación de Materias Primas (ERMP) de Cienfuegos, Cuba, de la cual se obtuvieron los costos y consumos de recursos asociados al transporte, los centros recolectores y la producción se muestran en la Tabla 1.

Para la evaluación de los impactos ambientales durante el ciclo de vida asociados al problema se utilizaron los análisis de ciclos de vida realizados y contenidos en la base de datos Ecoinvent 3. La muestra los valores de los impactos ambientales utilizados para este caso de estudio, la selección del Ecoindicador 99 está dada debido a que este método de evaluación del impacto ambiental es uno de los más difundidos y está incluido en las bases de datos y programas computacionales que realizan análisis de ciclos de vida.

Las soluciones del modelo se ejecutaron utilizando el paquete de optimización Opti desarrollado para MatLab, capaz de lidiar con problemas de programación no lineal entera mixta (MINLP). El solucionador seleccionado es el Solving Constraint Integer Programs (SCIP) debido a que está implementado para resolver problemas lineales y no lineales enteros y mixtos.

En función de construir el conjunto de soluciones se determinaron 20 límites para la restricción de la función del ahorro medioambiental, calculados desde el valor mínimo hasta el máximo de la función en la matriz de pago y 5 para la cantidad de plástico vendido total, lo que equivale a 100 optimizaciones.

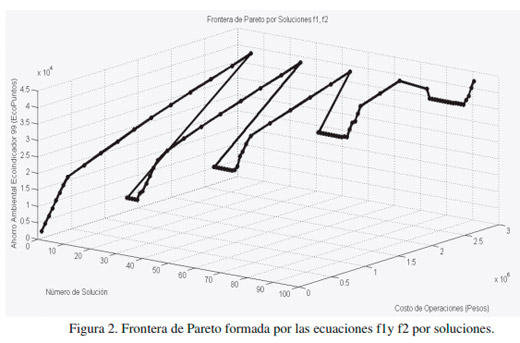
Una vez realizadas las corridas del modelo, se muestra en la Figura 2 la frontera de Pareto formada por las funciones objetivos f1 y f2 para cada solución. En la misma se puede observar cómo, a medida que aumenta el ahorro medioambiental por utilizar materiales reciclados, el costo de operación de la cadena aumenta al principio con menor pendiente, luego más aceleradamente debido a la necesidad de utilizar más instalaciones y recursos para la producción y transporte entre más eslabones. Los saltos constituyen las cantidades mínimas vendidas, lo que constituye el parámetro del término independiente de la restricción formada por la función objetivo f3. Para los puntos 20, 40, 60, 80 y 100 el modelo no encontró soluciones factibles por lo que los valores de las variables y de las funciones objetivo son 0, estas fueron eliminadas del gráfico que representa la frontera de Pareto.

Selección de las soluciones

Con el fin de brindar información relevante al centro decisor se pueden representar algunos indicadores de interés a partir de las relaciones entre las funciones objetivo y otros resultados. En Figura 3 se muestran en las barras, las cantidades de plástico recuperadas, vendidas y el inventario resultante al final del período así como la relación entre el costo de operaciones y el ahorro ambiental que se alcanzaría con cada solución. Las soluciones 19, 39, 59, 79 y 99 resultan interesantes, pues aunque el costo por cada punto del ecoindicador es alto comparado con otras, son las configuraciones de la cadena de suministro en que más plásticos totales se recuperan y se vende para cada subgrupo de soluciones. Este conjunto de soluciones pudiera ser aceptado si la estrategia de la empresa estuviera enfrascada en obtener altos niveles de servicio al cliente a pesar del costo.

Otros puntos de interés para la toma de decisiones pueden ser las soluciones 8, 30, 54, 76 y 99 debido a que constituyen los puntos de más bajo costo en relación con el impacto ambiental positivo. Si los decisores prefieren la eficiencia en el logro ambiental y obtener buenos indicadores medioambientales a bajos costos de operación, este subconjunto de soluciones reviste particular importancia. Si se analiza la Figura 3 se puede observar como las soluciones de la 1 a la 13 y de la 28 a la 33 mejoran el costo por ahorro ambiental recuperando más de lo que se procesa y acumulando inventario. Generalmente esas soluciones brindan las mejores relaciones costos-impactos ambientales, pero tienen pocas ventas y por tanto poca producción, demostrando que los mayores costos se generan por transportar y producir. Este grupo de soluciones por lo general no son atractivas para los decisores, pues aunque presentan bajos costos de operaciones se obtienen pocos beneficios económicos.

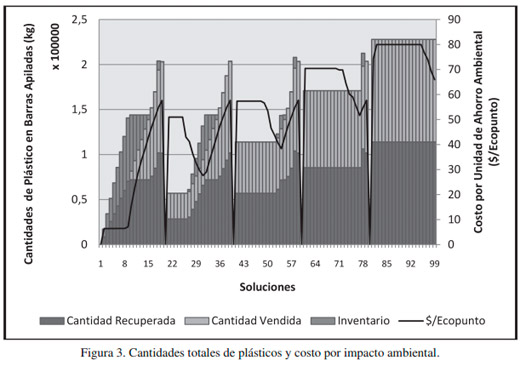
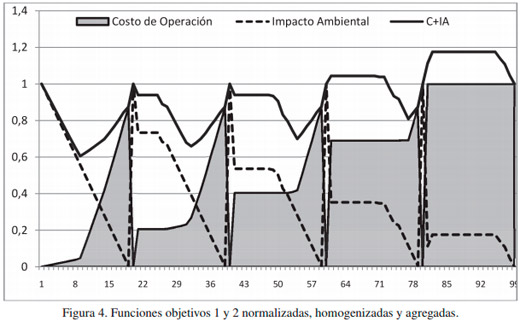
Para comparar con los costos de operaciones se restó del máximo, cada valor del impacto ambiental del conjunto de soluciones para que ambas funciones se encuentren homogéneas en relación con el objetivo de minimizarse. Además se normalizaron los valores de los resultados utilizando la división de cada valor entre el máximo y se formó la función agregada de ambas funciones como se muestran en la Figura 4. Al analizar este gráfico se pueden notar que los puntos 9, 33, 54, 77 y 99 constituyen las configuraciones de la cadena que mejor desempeño conjunto tienen los dos objetivos f1 y f2, y pudieran ser interesantes para los decisores.

CONCLUSIONES

Las actividades comprendidas en logística inversa son vitales para la sostenibilidad de las cadenas de suministros, siendo su diseño una de las decisiones más estudiadas por su importancia estratégica para la gestión eficiente de las mismas. Los esfuerzos de integrar la dimensión medioambiental a la económica, en los modelos para el diseño de las cadenas de suministros inversas, aún son escasos en la literatura, predominando el uso del LCA como herramienta de evaluación del impacto ambiental.

Por ello, resultaba necesario el desarrollo de un modelo que represente la situación específica de cadenas de recolección de múltiples productos, adecuada al caso de las ERMP cubanas.

El modelo propuesto resulta un novedoso aporte para el diseño de las cadenas de suministros sostenibles de reciclaje puesto que integra objetivos económicos y ambientales, soporta varias decisiones tácticas y estratégicas como localización de instalaciones, diseño del flujo material y asignación de transporte.

La función objetivo que representa el impacto ambiental es capaz de interpretar mejor que las revisadas en la literatura el compromiso entre la apertura de instalaciones y el uso del transporte lo cual constituye una novedad.

El uso de un conjunto de indicadores de interés a partir de las relaciones de las funciones objetivo como las cantidades recuperadas, vendidas e inventario sobrante y el costo por cada punto de ahorro del impacto ambiental constituyen un valioso soporte al proceso de toma de decisiones. A partir de estos indicadores se pudo reducir notablemente el número de soluciones atractivas para los decisores.

Se debe continuar la investigación desarrollando métodos que permitan evaluar la sensibilidad de las soluciones ante diferentes escenarios debido a la naturaleza estocástica de algunos parámetros como son la demanda y la generación de los materiales reciclables. El desarrollo de funciones que describan el comportamiento social de las cadenas e integrarlas en los modelos cuantitativos para el diseño constituye otro posible camino para seguir profundizando en esta investigación.

REFERENCIAS

[1] WCED. “Our common future: Report of the World Commission on Environment and Development”. Oxford: Oxford University Press. Brundtland, pp. 23. 1987.

[2] A.M. Hasna. “Sustainability classifications in engineering: discipline and approach”. International Journal of Sustainable Engineering. Vol. 3 Nº 4, pp. 258-276. 2010.

[3] L.M.A. Bettencourt and J. Kaur. “Evolution and structure of sustainability science”. Proceedings of the National Academy of Sciences. Vol. 108 Nº 49, pp. 19540-19545. 2011.

[4] S. Sala, F. Farioli and A. Zamagni. “Life cycle sustainability assessment in the context of sustainability science progress (part 2)”. The International Journal of Life Cycle Assessment. Vol. 18 Nº 9, pp. 1686-1697. 2013.

[5] S. Sala, F. Farioli and A. Zamagni. “Progress in sustainability science: lessons learnt from current methodologies for sustainability assessment: Part 1”. The International Journal of Life Cycle Assessment. Vol. 18 Nº 9, pp. 1653-1672. 2013.

[6] J.M. Rabadán Vergara and M. Luffiego García. “La evolución del concepto de sostenibilidad y su introducción en la enseñanza”. Enseñanza de las Ciencias. Vol. 18 Nº 3, pp. 473-486. 2000.

[7] M. Starik and G.P. Rands. “Weaving an integrated web: Multilevel and multisystem perspectives of ecologically sustainable organizations”. Academy of Management Review. Vol. 20 Nº 4, pp. 908-935. 1995.

[8] C.R. Carter and D.S. Rogers. “A framework of sustainable supply chain management: moving toward new theory”. International journal of physical distribution & logistics management. Vol. 38 Nº 5, pp. 360-387. 2008.

[9] E. Hassini, C. Surti and C. Searcy. “A literature review and a case study of sustainable supply chains with a focus on metrics”. International Journal of Production Economics. Vol. 140 Nº 1, pp. 69-82. 2012.

[10] J. Elkington. “Cannibals with forks: The triple bottom line of sustainability”. Gabriola Island: New Society Publishers. Vol. Nº pp.  1998.

[11] S. Seuring and M. Müller. “From a literature review to a conceptual framework for sustainable supply chain management”. Journal of Cleaner Production. Vol. 16 Nº 15, pp. 1699-1710. 2008.

[12] S. Pokharel and A. Mutha. “Perspectives in reverse logistics: a review”. Resources, Conservation and Recycling. Vol. 53 Nº 4, pp. 175-182. 2009.

[13] M. Feitó Cespón and R. Cespón Castro. “Estudio empírico sobre las estrategias de logística inversa en el sector industrial de la provincia de Villa Clara”. Ingeniería Industrial. Vol. 30 Nº 3, pp. 2010.

[14] F. Hevia Lanier. “Metodología de diseño de la cadena de suministro inversa”. Tesis en opción al grado científico de doctor. Instituto Superior Politécnico “José Antonio Echeverría”. La Habana, Cuba. 2008

[15] M. Feitó Cespón, R. Cespón Castro and J. Lundquist. “Empiric Study on Reverse Logistic Strategies in the Manufacturing Sector in the Central Area of Cuba”. Journal of Operations and Supply Chain Management. Vol. 2 Nº 2, pp. 72-82. 2013.

[16] K. Das and A.H. Chowdhury. “Designing a reverse logistics network for optimal collection, recovery and quality-based product-mix planning”. International Journal of Production Economics. Vol. 135 Nº 1, pp. 209-221. 2012.

[17] Y. Kristianto, A. Gunasekaran, P. Helo and M. Sandhu. “A decision support system for integrating manufacturing and product design into the reconfiguration of the supply chain networks”. Decision Support Systems. Vol. 52 Nº 4, pp. 790-801. 2012.

[18] F. Toyasaki, P. Daniele and T. Wakolbinger. “A variational inequality formulation of equilibrium models for end-of-life products with nonlinear constraints”. European Journal of Operational Research. Vol. 236 Nº 1, pp. 340-350. 2014.

[19] P.-A. Yvars. “A CSP approach for the network of product lifecycle constraints consistency in a collaborative design context”. Engineering Applications of Artificial Intelligence. Vol. 22 Nº 6, pp. 961-970. 2009.

[20] N. Aras and D. Aksen. “Locating collection centers for distance- and incentive-dependent returns”. International Journal of Production Economics. Vol. 111 Nº 2, pp. 316-333. 2008.

[21] N. Aras, D. Aksen and A. Gönül Tanu ur. “Locating collection centers for incentivedependent returns under a pick-up policy with capacitated vehicles”. European Journal of Operational Research. Vol. 191 Nº 3, pp. 1223-1240. 2008.

[22] J.N. de Figueiredo and S.F. Mayerle. “Designing minimum-cost recycling collection networks with required throughput”. Transportation Research Part E: Logistics and Transportation Review. Vol. 44 Nº 5, pp. 731-752. 2008.

[23] Z.-H. Hu. “A container multimodal transportation scheduling approach based on immune affinity model for emergency relief”. Expert Systems with Applications. Vol. 38 Nº 3, pp. 2632-2639. 2011.

[24] S. Molla-Alizadeh-Zavardehi, M. HajiaghaeiKeshteli and R. Tavakkoli-Moghaddam. “Solving a capacitated fixed-charge transportation problem by artificial immune and genetic algorithms with a Prüfer number representation”. Expert Systems with Applications. Vol. 38 Nº 8, pp. 10462-10474. 2011.

[25] G. Zacharewicz, J.-C. Deschamps and J. Francois. “Distributed simulation platform to design advanced RFID based freight transportation systems”. ICT for Sustainability in Industry. Vol. 62 Nº 6, pp. 597-612. 2011.

[26] A. Chaabane. “Multi-criteria methods for designing and evaluating sustainable supply chains”. PhD. Thesis. Université du Quebéc. Montreal. 2011

[27] A. Chaabane, A. Ramudhin and M. Paquet. “Design of sustainable supply chains under the emission trading scheme”. Advances in Optimization and Design of Supply Chains. Vol. 135 Nº 1, pp. 37-49. 2012.

[28] J.Q. Frota Neto, J.M. Bloemhof-Ruwaard, J. Van Nunen and E. Van Heck. “Designing and evaluating sustainable logistics networks”. International Journal of Production Economics. Vol. 111 Nº 2, pp. 195-208. 2008.

[29] J. Quariguasi Frota Neto, G. Walther, J. Bloemhof, J.A.E.E. van Nunen and T. Spengler. “A methodology for assessing eco-efficiency in logistics networks”. European Journal of Operational Research. Vol. 193 Nº 3, pp. 670-682. 2009.

[30] M.S. Pishvaee and J. Razmi. “Environmental supply chain network design using multiobjective fuzzy mathematical programming”. Applied Mathematical Modelling. Vol. 36 Nº 8, pp. 3433-3446. 2012.

[31] C.R. Carter and P.L. Easton. “Sustainable supply chain management: evolution and future directions”. International journal of physical distribution & logistics management. Vol. 41 Nº 1, pp. 46-62. 2011.

[32] D. Kannan, A. Diabat, M. Alrefaei, K. Govindan and G. Yong. “A carbon footprint based reverse logistics network design model”. Resources, Conservation and Recycling. Vol.  67 Nº  pp.  75-79. 2012. [33] F. Dehghanian and S. Mansour. “Designing sustainable recovery network of end-of-life products using genetic algorithm”. Resources, Conservation and Recycling. Vol. 53 Nº 10, pp. 559-570. 2009.

Por: Michael Feitó Cespón, Roberto Cespón Castro, Manuel Alejandro Rubio Rodríguez

Fuente: Ingeniare. Revista chilena de ingeniería

VER ARCHIVO DE ARTÍCULO