Solicitar presupuesto

Modelos de difusión atmosférica – Parte 04

Parámetros de dispersión para una fuente puntual

Las ecuaciones que aproximan las curvas de Pasquill-Gifford (Turner, 1970) se usan en el cálculo de y y z (en metros) para el modo rural. Las ecuaciones usadas para calcular y son de la forma:

donde

En las ecuaciones anteriores la distancia en la dirección del viento x es en kilómetros, y los coeficientes c y d se obtienen de la tabla 1-1. La ecuación usada para determinar z es de la forma:

donde la distancia en la dirección del viento x es en kilómetros y z está expresada en metros. Los coeficientes a y b se obtienen de la tabla 1-2.

Las tablas 1-3 y 1-4 muestran las ecuaciones usadas para determinar y y z para la opción urbana. Estas expresiones fueron determinadas por Briggs (1976) y representan una mejor aproximación para los datos de difusión vertical urbana expuestos por McElroy y Poole (1968).

Tabla 1-1

Parámetros usados para el cálculo según PASQUILL-GIFFORD de y

Clase de estabilidad Pasquill

c

d

A

24.1670;

2.5334

B

18.3330;

1.8096

C

12.5000

1.0857

D

8.3330

0.72382

E

6.2500

0.54287

F

4.1667

0.36191

donde y está expresada en metros y x en kilómetros.

Tabla 1-2

Parámetros usados para el cálculo según PASQUILL-GIFFORD de z

Clase de estabilidad Pasquill

x (km)

a

b

A*

<0.10
0.10 – 0.15
0.16 – 0.20
0.21 – 0.25
0.26 – 0.30
0.31 – 0.40
0.41 – 0.50
0.51 – 3.11
> 3.11

122.800
158.080
170.220
179.520
217.410
258.890
346.750
453.850
**

0.94470
1.05420
1.09320
1.12620
1.26440
1.40940
1.72830
2.11660
**

B*

<0.20
0.21 – 0.40
> 0.40

1.0857
98.483
109.300

0.93198
0.98332
1.09710

C*

A11

61.141

0.91465

D

<0.30
0.31 – 1.00
1.01 – 3.00
3.01 – 10.00
10.01 – 30.00
> 30.00

34.459
32.093
32.093
33.504
36.650
44.053

0.86974
0.81066
0.64403
0.60486
0.56589
0.51179

E

< 0.10
0.10 – 0.30
0.31 – 1.00
1.01 – 2.00
2.01 – 4.00
4.01 – 10.00
10.01 – 20.00
20.01 – 40.00
> 40.00

24.260
23.331
21.628
21.628
22.534
24.703
26.970
35.420
47.618

0.83660
0.81956
0.75660
0.63077
0.57154
0.50527
0.46713
0.37615
0.29592

F

< 0.20
0.21 – 0.70
0.71 – 1.00
1.01 – 2.00
2.01 – 3.00
3.01 – 7.00
7.01 – 15.00
15.01 – 30.00
30.01 – 60.00
> 60.00

15.209
14.457
13.953
13.953
14.823
16.187
17.836
22.651
27.074
34.219

0.81558
0.78407
0.68465
0.63227
0.54503
0.46490
0.41507
0.32681
0.27436
0.21716

donde z está expresada en metros y x en kilómetros
* Si el valor calculado de z excede 5000m, z se toma igual a 5000m
** z es igual a 5000m

Tabla 1-3

Fórmulas de Briggs usadas para el cálculo de y de McElroy-Pooler

Clase de estabilidad Pasquill

y (metros)

A

0.32 x (1.0 + 0.0004 x)-1/2

B

0.32 x (1.0 + 0.0004 x)-1/2

C

0.22 x (1.0 + 0.0004 x)-1/2

D

0.16 x (1.0 + 0.0004 x)-1/2

E

0.11 x (1.0 + 0.0004 x)-1/2

F

0.11 x (1.0 + 0.0004 x)-1/2

* donde x está expresada en metros

Tabla 1-4

Fórmulas de Briggs usadas para el cálculo de z de McElroy-Pooler

Clase de estabilidad Pasquill

z (metros)

A

0.24 x (1.0 + 0.0004 x)-1/2

B

0.24 x (1.0 + 0.0004 x)-1/2

C

0.20 x

D

0.14 x (1.0 + 0.0004 x)-1/2

E

0.08 x (1.0 + 0.0004 x)-1/2

F

0.08 x (1.0 + 0.0004 x)-1/2

* donde x está expresada en metros

Distancias virtuales lateral y vertical

Las ecuaciones en las tablas 1-1, 1-2, 1-3 y 1-4 definen los parámetros de dispersión para una fuente puntual ideal. Por supuesto, las fuentes volumétricas tienen unas dimensiones lateral y vertical iniciales. También, como se ha discutido, los efectos de apantallamiento por edificios pueden incrementar el desarrollo inicial de los penachos de chimeneas. En estos casos, las distancias virtuales lateral (xy) y vertical (xz) serán añadidas por en el modelo a la distancia en el sentido del viento actual x para los cálculos de y y z. La distancia virtual lateral en kilómetros para el modo rural viene dado por:

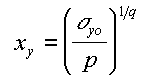
donde los coeficientes p y q vienen dados en la tabla 1-5 y y0 es la desviación estándar en metros de la distribución de la concentración lateral en la fuente. De forma similar la distancia vertical virtual en kilómetros para el modo rural viene dado por:

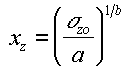
donde los coeficientes a y b se obtienen de la tabla 1-2 y z0 es la desviación estándar en metros de la distribución vertical de la concentración en la fuente. Es importante observar que el modelo ha de compruebar que la xz usada para calcular z en (x+xz) en el modo rural es la xz calculada usando los coeficientes a y b que corresponden a la categoría de distancia especificada por la cantidad (x+xz).

Para determinar las distancias virtuales en el modo urbano, las funciones mostradas en las tablas 1-3 y 1-4 se resuelven para x. Las soluciones son fórmulas cuadráticas para las distancias virtuales laterales; y para las distancias verticales virtuales las soluciones son ecuaciones cúbicas para las clases de estabilidad A y B, una ecuación lineal para la clase de estabilidad C y ecuaciones cuadráticas para las clases D, E y F. Las ecuaciones cúbicas son resueltas por iteración usando el método de Newton.

Tabla 1-5
Coeficientes usados para calcular las distancias virtuales laterales

Clase de estabilidad de Pasquill

p

q

A

209.14

0.890

B

154.46

0.902

C

103.26

0.917

D

68.26

0.919

E

51.06

0.912

F

33.92

0.919

Etiquetas