Modelos de difusión atmosférica – Parte 02
|
Parámetro de estabilidad
|
Para situaciones estables, el parámetro de estabilidad, s, se calcula con la ecuación (Briggs, 1971, p. 1031):
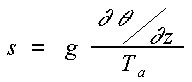
Como aproximación por defecto, para la clase de estabilidad E (o 5) ![]() se toma como 0.020 K/m, y para la clase F (o 6)
se toma como 0.020 K/m, y para la clase F (o 6) ![]() , se considera 0.035 K/m.
, se considera 0.035 K/m.
|
Parámetro de estabilidad
|
Para casos con temperatura del gas en la chimenea mayor o igual a la temperatura ambiental, se debe determinar cuando domina la fuerza ascensional o la cantidad de movimiento. El incremento de temperatura límite,![]() , se determina como sigue:
, se determina como sigue:
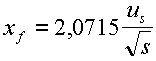
Si la diferencia entre la temperatura del gas en la chimenea y la temperatura ambiental, ![]() , excede o iguala
, excede o iguala ![]() , la elevación del penacho se asume que esta dominada por las fuerzas ascensionales, en otro caso se supone dominado por la cantidad de movimiento.
, la elevación del penacho se asume que esta dominada por las fuerzas ascensionales, en otro caso se supone dominado por la cantidad de movimiento.

|
Estable. Elevación por fuerza ascensional
|
Para situaciones donde ![]() excede
excede ![]() , como se determinó anteriormente, la fuerza ascensional se supone dominante. La distancia final de ascensión,
, como se determinó anteriormente, la fuerza ascensional se supone dominante. La distancia final de ascensión, ![]() , se determina por el equivalente de la combinación de las ecuaciones 48 y 59 en Briggs (1975, p. 96):
, se determina por el equivalente de la combinación de las ecuaciones 48 y 59 en Briggs (1975, p. 96):
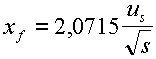
La altura del penacho, ![]() , se determina por el equivalente de la ecuación 59 de Briggs (1975, p. 96):
, se determina por el equivalente de la ecuación 59 de Briggs (1975, p. 96):
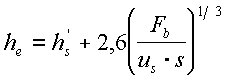
|
Estable. Elevación por cantidad de movimiento
|
![]()
, se asume también que la elevación del penacho está dominada por la cantidad de movimiento. La altura del penacho se calcula con la ecuación 4.28 de Briggs (1969, p.59):
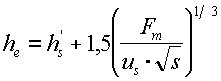
La ecuación para la elevación por cantidad de movimiento en el caso inestable-neutro también se eval&;a. El menor resultado obtenido de estas dos ecuaciones es la altura resultante del penacho, puesto que la elevación del penacho en condiciones de estabilidad no puede superar al caso inestable-neutro.