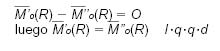La biomecánica en el transporte humano de cargas. Parte 1

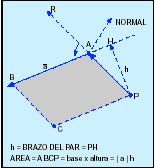
Resultante de un sistema de vectores es la suma de éstos.
Momento de un vector a (AB) respecto a un punto P es un vector cuyo módulo es el área del paralelogramo formado por los vectores PB y AB y las rectas paralelas a éstos que pasan por los puntos B y P, o también el producto del brazo del par (distancia del punto P a la recta a acción del vector AB por el módulo de |a |.

Dirección, perpendicular al plano formado por los puntos A B P.
El sentido nos lo da la regla del sacacorchos al llevar el primer vector PA sobre el segundo A B.

Dos sistemas de vectores deslizantes son equivalentes cuando tienen la misma resultante y el mismo momento resultante respecto a un punto. Si esto ocurre, la igualdad de momentos se verifica respecto a todos los puntos del espacio.

Demostración
El momento resultante Mp (R) de un sistema S de vectores deslizantes respecto a un punto P es igual al momento resultante respecto al origen Mo (R) más el momento de la resultante aplicada en O respecto a P.

Sean dos sistemas de vectores S’ y S’’, cuyas resultantes R’ y R’’ son iguales, y los momentos resultantes respecto al punto P son iguales

Vamos a demostrar que los momentos resultantes respecto a otro punto O son iguales:

restando y teniendo en cuenta

nos queda

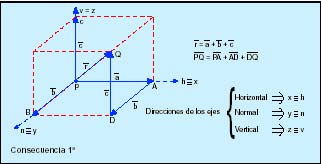
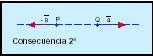
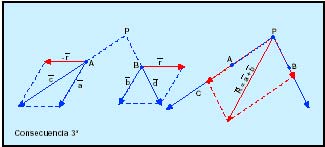
Consecuencias

1ª. Un vector r aplicado en un punto P se puede sustituir por un sistema de vectores equivalentes a r, formado por varios vectores a, b y c situados sobre rectas concurrentes en el punto P y cuya suma vectorial sea igual a éste, es decir, que la poligonal formado por estos vectores cierre el vector r:

2ª. Un sistema de vectores es equivalente a cero cuando su resultante y el momento resultante respecto a cualquier punto son nulos. Un sistema nulo está constituido por dos vectores, iguales, opuestos y situados sobre la misma recta. De donde se deduce que si a un sistema de vectores se le añade un sistema nulo, resulta un sistema equivalente al primero.

3ª. Un sistema de vectores deslizantes paralelos o concurrentes en un punto se puede sustituir por su vector resultante aplicado en cualquier punto del eje central (es el lugar de los puntos con respecto a los que la proyección del momento resultante del sistema sobre dicho eje es mínima).

Si los vectores son paralelos, el momento resultante es perpendicular a esta dirección, por lo que su proyección es nula. Si son concurrentes, el momento respecto al punto de intersección es nulo.

Ejemplo: sean dos vectores paralelos a y b aplicados en los punto A y B. Si trazamos por estos puntos una recta sobre la cual situamos un sistema nulo r y r, el sistema que resulta c y d es equivalente al anterior y podemos sustituirlo por la resultante aplicada en la intersección de c y d, P y cuya suma será a + b = R.

4ª. Un sólido rígido sometido a un sistema de fuerzas exteriores está en equilibrio cuando la resultante de éstas y su momento resultante respecto a cualquier punto del espacio son nulos.

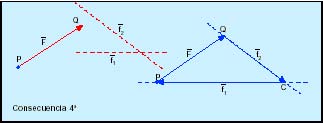
La condición necesaria para que esto se verifique es que todas éstas fuerzas pasen por un punto y que la poligonal formada por éstas sea cerrada. A partir de esto se deduce:
Si de tres fuerzas coplanarias concurrentes en un punto conocemos una F (PQ) en magnitud, dirección y sentido, y de las otras f1 y f2 sólo su dirección, podemos determinar su magnitud y sentido a partir de la siguiente construcción gráfica:

Trazar por el punto P una recta paralela a f1 y por Q, otra paralela a f2. El punto intersección C de ambas nos dará la solución, pues el polígono de fuerzas debe ser cerrado y, por lo tanto, la resultante nula.

Apartados

– Si en un sistema cualquiera de vectores tenemos dos iguales y opuestos, misma dirección y sobre una misma recta, podemos suprimirlos, pues constituyen un sistema nulo.
– El movimiento de un sólido rígido sometido a fuerzas exteriores se puede sustituir siempre por una traslación y una rotación.

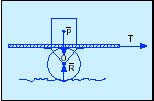
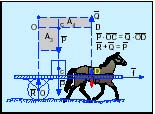
El traslado de cargas antes de la invención de la rueda por el hombre se hacía empujando los cuerpos sobre las superficies de deslizamiento, lo que resultaba más fácil cuando se trataba de grandes pesos. Las películas nos recuerdan la forma con que los indios llevaban los fardos y bártulos al cambiar de asentamiento mediante el uso de caballerías.

En la actualidad se sabe que las fuerzas de rozamiento por fricción entre dos cuerpos de contacto comprimidos uno contra otro por una fuerza N, normal a la superficie de contacto, ofrecen al deslizamiento una resistencia tangencial proporcional a N, independiente del área de las superficies de contacto y distinta según la naturaleza de las superficies (material, pulimento, lubricación, humedad, etc.), es decir, que la fuerza de rozamiento Fr, es igual a la fuerza normal N, multiplicada por un coeficiente K, llamado de rozamiento por deslizamiento.

Éste puede ser estático o cinético, según el cuerpo esté en reposo o en movimiento, siendo el estático mayor que el cinético. (En los concursos de desplazamiento de grandes piedras, utilizando la ayuda de parejas de bueyes, en el norte, el que dirige la prueba trata de que no se pare la piedra, puesto que necesitaría una mayor energía para volver a iniciar el movimiento.)

Con respecto a la resistencia a la rodadura, un cilindro no rueda hasta que no se le aplica un par de fuerzas que supere un cierto valor M, siendo M proporcional a la fuerza que comprime el cilindro contra la superficie de rodadura, dependiendo, además, de la clase y estado de las superficies:

Siendo el coeficiente de rodadura, y que tiene la dimensión de una longitud. Éste puede ser: estático o cinético, siendo el primero mayor que el segundo. El coeficiente de rozamiento por deslizamiento es mucho mayor que el de rodadura, por lo que la resistencia que opone un cuerpo a deslizarse es mucho mayor que si se transporta sobre ruedas. Actualmente, el movimiento de grandes pesos, como botar barcos, etc., se hace por medio de rodillos, con lo que se sustituye el deslizamiento por la rodadura, con una resistencia mucho menor.

En la figura 1, el sistema está en equilibrio, pues el peso P y la reacción R, al estar alineados y opuestos, constituyen un sistema nulo. Par mover el carro se debe aplicar, pues, una fuerza horizontal f que sea mayor que la fuerza de resistencia a la rodadura.

Figura 1

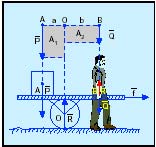
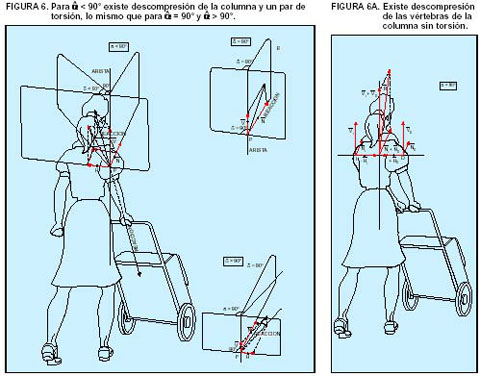
Para que un sistema esté en equilibrio debe verificarse que la suma de los momentos de las fuerzas aplicadas P, F y R respecto a O, sean nulos (R al pasar por O, su momento es nulo), además de que su resultante deberá ser cero. P+ F+ R= O

Como los momentos representan rotaciones alrededor del eje horizontal que pasa por O, sus módulos son equivalentes a las áreas de los rectángulos formados por el brazo del par y el vector correspondiente, es necesario que éstas sean iguales, es decir, A1 = A2.

En la figura 2 las fuerzas P y F están a distinto lado del eje de giro aplicadas, respectivamente, en los puntos A y B. En el punto B se debe empujar hacia abajo, para evitar que el mástil se levante, por lo que aparecerá una reacción que afectará a la columna vertebral, produciendo su descompresión. Si el peso P, estuviera más alejado de O, podría levantar al portador.

figura 2 figura 3

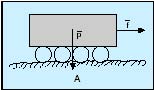
En la figura 3 las fuerzas P y F están a un mismo lado de O, aplicadas, respectivamente, en los puntos C y D. En este último punto se originará una reacción análoga al caso anterior, pero hacia el suelo, con lo que la acémila que tira del carro tendrá un mayor peso, por lo que aumentará la resistencia al deslizamiento en sus patas y podrá desplazarse con más facilidad.

Por eso, el carretero suele sentarse sobre un mástil para aumentar el peso del animal, con lo que este tendrá más agarre.

En el caso de las carreteras con cuatro ruedas sólo se debe vencer la resistencia a la rodadura, por lo que, cuando el peso transportado es muy grande, se engancharán varias caballerías para facilitar su movimiento (Fig. 4A).

figura 4

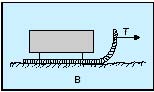
En los trenes, cuando deben vencer pendientes muy acentuadas, se enganchan varias locomotoras para poder subirlas.

Tanto en las carretas como en los carros, las ruedas son de gran tamaño, ya que al tener un radio de curvatura mayor se pueden vencer con más facilidad los obstáculos que puedan presentarse en el camino.

Existen otros medios para el transporte de cargas. Sobre rodillos, en los que se sustituye el deslizamiento por la rodadura, con lo que disminuye el rozamiento. (Fig. 4B).

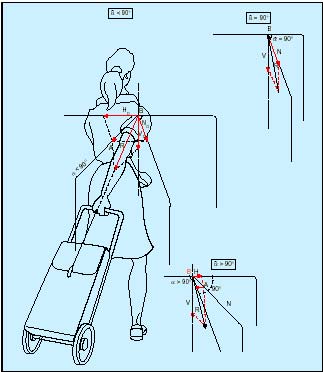
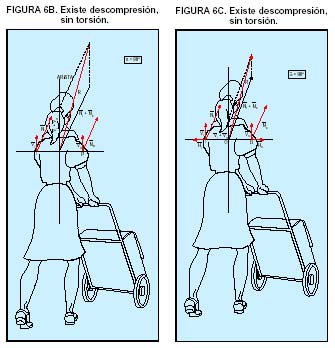
Sobre nieve se utilizan trineos, que con el deslizamiento se evita el hundimiento de las ruedas y, por tanto, su bloqueo. En el transporte mediante orugas, al ser mayor el radio de curvatura, permite sortear obstáculos con más facilidad y al aumentar la superficie, lo que impide el hundimiento en el terreno. Para aumentar la adherencia, se colocan en las bandas rodantes unos salientes, que permiten al clavarse en el suelo, facilitar el avance. (Fig. 4C).

En el transporte de pesos con el carro de la compra se descompone la reacción entre direcciones y componentes: horizontal, normal y vertical, de las que se sacan las siguientes conclusiones: