Guía para el diseño… 11. Apéndice E

..:: Una solución para la disposición final de
residuos sólidos municipales en pequeñas poblaciones ::..

Centro Panamericano de Ingeniería Sanitaria y Ciencias del Ambiente
División de Salud y Ambiente
Organización Panamericana de la Salud
Oficina Sanitaria Panamericana, Oficina Regional de la
Organización Mundial de la Salud
2002

Cálculo de la capacidad volumétrica del sitio

E.1 Cálculo de áreas

El área de cualquier figura que se haya levantado puede calcularse a partir de:

• Las anotaciones de campo
• El plano dibujado

E.1.1 Áreas deducidas de las notas de campo

• Levantamientos con cinta métrica

En un levantamiento con cinta métrica, el área se subdivide en triángulos cuyos tres lados se miden y el área de cada uno se encuentra por la fórmula (figura E.1):

Área = [ s (s – a) (s – b) (s – c) ]½

Donde:
s = semiperímetro; es decir:

a, b, c= lados del triángulo

Ejemplo 1:

En la figura E.1 se ve un sencillo levantamiento con cinta, compuesto en parte por el triángulo PQR, cuyos lados miden:

PQ = 60,0 m
QR = 104,6 m
RP = 70,0 m

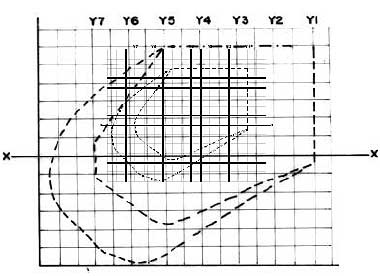Figura E.1 Levantamiento de un terreno con cinta métrica

El área del PQR se halla así:

a. En el triángulo PQR:

• PQ = r = 60,0 m
• QR = p = 104,6 m
• RP = q = 70,0 m

Perímetro de PQR = 234,6 m
por tanto, semiperímetro s = 117,3 m

b.

• s – r = 57,3
• s – p = 12,7
• s – q = 47,3

Comprobación = 117,3 = s

c. Area del triángulo PQR = ????s(s – r) (s – p) (s – q)
= ???117,3 x 5,7,3 x 12,7 x 47,3
= 2.009,3 m²

Los linderos se hallaron por medio de desvíos desde los alineamientos.

En la figura 5.1 el área entre la línea del levantamiento y el arroyo está formada por una sucesión de triángulos y trapecios, cuyas áreas pueden calcularse separadamente así:

Sobre la línea RQ :
Área del triángulo (1) = ½ x 19 x 4 = 38,0
Área del trapecio (2) = ½ (4+8) x (38 – 19) = 114,0
Área del trapecio (3) = ½ (8+4,5) x (55 – 38) = 106,25
Área del rectángulo (4) = 4,5 x (72-55) = 76,5
Área del trapecio (5) = ½ (4,5 + 7) x (87 – 72) = 86,25
Área del triángulo (6) = ½ (104,6 – 87) x 7 = 61,6

4 8 2 , 6 m 2

El área entre la línea PQ y el camino también está formada por triángulos y trapecios. Sin embargo, en este caso, los desvíos están a intervalos regulares de 10 metros.

Llamando Y a cada desvío, el área entre dos desvíos consecutivos cualesquiera se calcula así:

Área entre abscisa 20 y abscisa 30 = ½(Y₂₀ + Y₃₀) x 10

Por tanto:

Área total = ½(Y_o + Y₁₀) x 10 + ½ (Y₁₀ + Y₂₀) x 10 + ½(Y₂₀ + Y₃₀) x 10 + …

+ ½(Y₅₀ + Y₆₀) x 10

= ½ x 10(Y_o + Y₁₀ + Y₁₀ + Y₂₀+ Y₂₀ + Y₃₀ + … + Y₅₀ + Y₆₀)

= ½ x 10(Y_o + Y₆₀ + 2Y₁₀ + 2Y₂₀ + 2Y₃₀ + 2Y₄₀ + 2Y₅₀)

= 10(Y_o + Y₆₀

+ Y₁₀ + Y₂₀ + Y₃₀ + Y₄₀ + Y₅₀)

Esta es la regla de los trapecios que se enuncia generalmente así:
Área = Ancho de la banda x (promedio del primero y último desvíos + suma de los demás)

d. En la figura 5.3 el área es como sigue:

El área puede hallarse con un poco más de precisión con la regla de Simpson, que puede enunciarse así:

Área = 1/3 del ancho de las bandas (primero + último desvíos + doble de la suma de los desvíos impares + cuádruplo de la suma de los desvíos pares).

Nota :
(i) Debe haber un número impar de desvíos.
(ii) Los desvíos deben darse a intervalos regulares.

Usando la regla de Simpson, el área entre la línea PQ y el camino será:

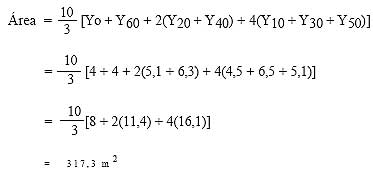e. Por último, se calcula el área entre el alineamiento RP y el bosque. El área se debe calcular mediante la regla de los trapecios, porque hay un número par de desvíos entre R y P a intervalos regulares de 10 metros.

El área entre las abscisas 70 m y 74 m se calcula por separado. El área entre RP y el bosque será:

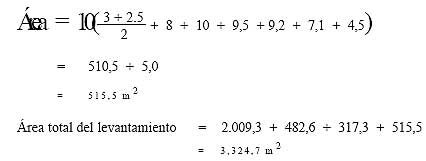E.1.2 Cálculo de las áreas a partir del plano

Se dispone de diversos métodos para hallar el área de una figura dada en un plano. Las áreas de las curvas de nivel se pueden medir con un planímetro, gráficamente, por la regla de Simpson o la de los trapecios. A continuación se describen los
tres últimos por considerarlos de muy fácil aplicación en estos casos.

• Mediante un planímetro

El área de cualquier figura irregular puede encontrarse en un plano utilizando el aparato mecánico para medir áreas conocido como planímetro.

• Cálculo del área gráficamente

Se coloca un pliego de papel transparente cuadriculado o milimetrado sobre el plano, se cuentan los cuadrados y se deduce el área.

• Por la regla de Simpson o la de los trapecios

Se subdivide el área en una serie de bandas de igual ancho, se miden las ordenadas correspondientes y se usa una u otra regla.

Ejemplo 2:

La figura E.2 muestra un área de forma irregular en un plano a escala 1:500. Calcular el área de la parte superior del relleno por los métodos gráficos y por las reglas de Simpson y de los trapecios.

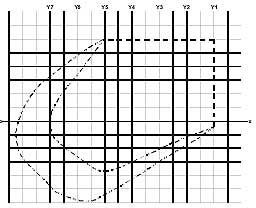Figura E.2 Cálculo del área por el método gráfico

Solución

a. Método gráfico

El papel transparente cuadriculado superpuesto al plano tiene cuadrados de 5 milímetros de lado y, por lo tanto, cada cuadrado representa un área en el terreno de:
( 5 x 500) mm² = 25 x 0,25 m² = 6,25 m²

Área = (6.25 x número de cuadrados) m²
= 6,25 x 89
= 556,25 m2

b. Regla de Simpson y de los trapecios

Supongamos la recta marcada xx como la línea de base y cada segunda línea vertical del papel cuadriculado como una ordenada Y de las que habrá siete en total (Y₁ a Y₇). Las longitudes de estas ordenadas, leídas a escala, son de 16 m, 18,3 m, 20 m, 22,5 m, 23,8 m, 15,3 m y 0 m, y su separación es de 5 m a lo largo de la línea de base.

Por la regla de Simpson:
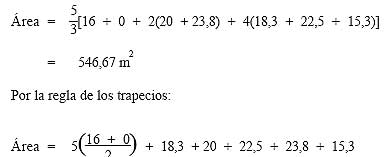