Guía para el diseño… 11. Apéndice D. Parte 2

..:: Una solución para la disposición final de
residuos sólidos municipales en pequeñas poblaciones ::..

Centro Panamericano de Ingeniería Sanitaria y Ciencias del Ambiente
División de Salud y Ambiente
Organización Panamericana de la Salud
Oficina Sanitaria Panamericana, Oficina Regional de la
Organización Mundial de la Salud
2002

Volumen del relleno sanitario de área

D.5 Ejemplo 5. Cálculo del volumen por la regla de Simpson

Supóngase un proyecto de relleno sanitario manual en un tramo de carretera abandonada cuyos cortes son similares a los mostrados en la figura siguiente y supóngase también que se han tomado niveles en ejes transversales a intervalos de 100 metros con una altura promedio de 8 metros.

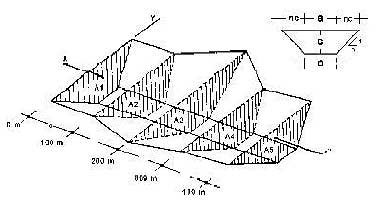Figura D.2 Configuración del terreno en el tramo de una carretera abandonada

El relleno tendrá un ancho a de 6 metros en el fondo, una pendiente variable en cada tramo y los siguientes datos:

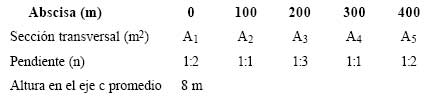La base mayor del trapecio será:

Ancho de la superficie del relleno = (a + nc + nc) metros
en cada abscisa (a = 6) = [6 + 2(nc)] metros

Por lo tanto, el área de la sección en cada abscisa (trapecio) será:

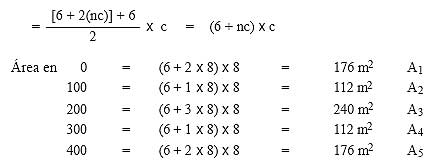Aplicando la regla de Simpson (ecuación 5-17):

D.6 Ejemplo 6. Cálculo del volumen por la regla del prismoide

En la figura se muestra un proyecto de relleno sanitario manual en un zanjón del que se conocen los siguientes datos:

i. longitud de la zanja 100 m
ii. ancho de la base inferior 6 m
iii. profundidad inicial 8 m
iv. profundidad final 5 m
v. taludes 1:1

Calcular el volumen del relleno por medio de la fórmula del prismoide:

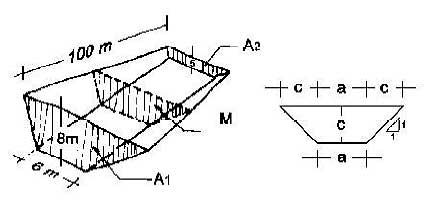Figura D.3 Relleno sanitario en un zanjón

Solución

i. Sección A1:

ancho de la base = 6m
ancho total = (6 + 2c) m
profundidad en el eje c = 8m
Por lo tanto, ancho total = (6 + 16) m = 22 m

ii. Sección A2:

ancho de la base = 6m
ancho total = (6 + 2c)
profundidad del eje c = 5m
Por lo tanto, ancho total = (6 + 10) m = 16 m

iii. Sección media M:

ancho de la base = 6m
ancho total = (6 + 2c) m
profundidad del eje c = promedio de profundidad en A1 y A2
= ½ (8 + 5) m
= 6,5 m

Por lo tanto, ancho total = 6 + 13 m = 19 m (promedio de los anchos en A1 y A2)

iv. Área de las secciones y trapecios
A1 = ½ (6 + 22) x 8 = 112 m2
A2 = ½ (6 + 16) x 5 = 55 m2
M = ½ (6 + 19) x 6,5 = 81,25 m2

v.

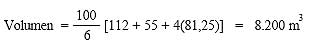D.7 Ejemplo 7. Volumen a partir de las áreas extremas

Partiendo de los mismos datos del ejemplo anterior, tenemos:

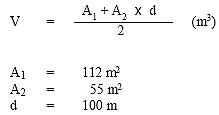Entonces, el volumen será:

Se observa que el resultado es aproximado.

D.8 Ejemplo 8. Volumen a partir de una retícula

En la figura se muestra una pequeña parte de una retícula. El área debe rellenarse hasta la cota 100,0 metros para obtener la superficie final. Los taludes se considerarán verticales.

El sólido con base en cada cuadro de la red es un prisma vertical truncado. Esto es, un prisma cuyas bases no son paralelas.

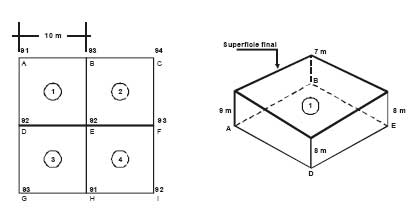Figura D.4 Terraplén con la forma de un prisma vertical truncado

Volumen de cada prisma = altura promedio x área de la base

La altura promedio de cada prisma truncado por debajo de la cota 100,0 m es de:

prisma 1 = (9 + 7 + 8 + 8) / 4 = 8 m
prisma 2 = (7 + 6 + 8 + 7) / 4 = 7 m
prisma 3 = (8 + 8 + 7 + 9) / 4 = 8 m
prisma 4 = (8 + 7 + 9 + 8) / 4 = 8 m

Área de la base de cada prisma truncado = 10 x 10 = 100 m2

Por lo tanto :

Volumen de 1 = 100 x 8 = 800 m3
2 = 100 x 7 = 700 m3
3 = 100 x 8 = 800 m3
4 = 100 x 8 = 800 m3
Volumen total disponible = 3.100 m3

También puede hallarse el volumen de la siguiente manera:

Volumen = altura promedio del relleno x área total

La altura promedio del relleno es el promedio de las alturas promedio de los prismas y no la media de las alturas en los puntos de nivel.

Altura promedio de relleno = (8 + 7 + 8 + 8) / 4 = 7,75 m
Área total = 20 x 20 = 400 m2
donde:

Volumen total = 7,75 x 400 = 3.100 m3

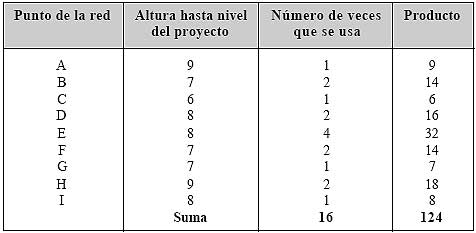Al observar en detalle este proceso, se ve que el nivel A se usó solo una vez para hallar la altura promedio del relleno, el nivel B dos veces y el E cuatro veces en total. En consecuencia, la altura promedio y el volumen pueden hallarse en forma más sencilla tabulando las operaciones como en la tabla anterior.

Las alturas en los puntos de nivel se tabulan en la columna 2 y el número de veces que se usan son tabulados en la 3; la columna 4 lista los productos de los números de las columnas 2 y 3; la altura media se halla dividiendo la suma de la columna 4 por la de la columna 3.

Altura media del relleno = 124 / 16 m
= 7,75 m como antes

D.9 Ejemplo 9. Volumen a partir de las curvas de nivel

El procedimiento consiste en determinar la capacidad existente del sitio, entre los planos horizontales de los terraplenes de basura que se pueden construir en el terreno, para lo cual es necesario calcular las áreas horizontales, obtener el promedio de la suma de las áreas y multiplicarlas por la diferencia de altura entre los planos horizontales.

Por lo tanto, el volumen del relleno está dado por la ecuación:

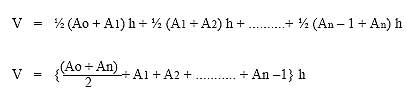Procedimiento:

1. Se prepara un plano del sitio a escala 1:250, 1:500 ó 1:1.000, de acuerdo con el tamaño del terreno, con las curvas de nivel de cada metro.
2. Se dibuja la topografía del terreno, después de la preparación inicial y la topografía final del relleno sanitario, asegurando la pendiente de la superficie (2 a 3%) para facilitar el drenaje del agua de lluvia.
3. Se traza un eje horizontal en el punto que sea conveniente y luego se corta el terreno con los planos horizontales A0, A1, A2, A3….. y An, con una altura h entre ellos. Se recomiendan 3, 5, 10 ó 15 m de distancia entre los planos horizontales, de acuerdo con el tamaño del terreno.
4. Se calculan las áreas A0, A1, A2, A3….. y An, usando los mapas de topografía inicial, final y los de avance de las etapas del relleno.
5. Se calcula la capacidad volumétrica del sitio, usando las ecuaciones 5-19, 5-20, 5-21 ó 5-22, tomando las áreas calculadas en el punto 4.

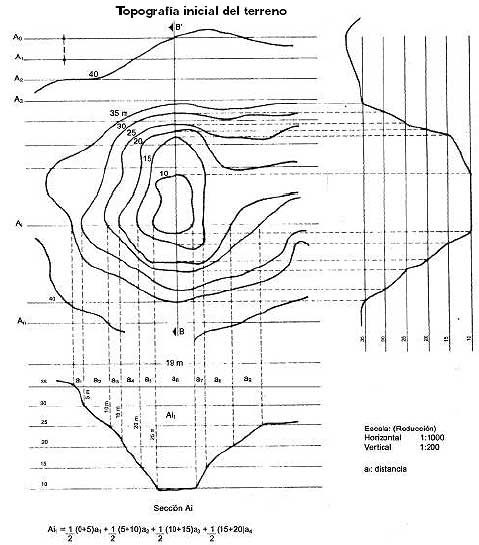Figura D.5 Planta y perfiles del terreno y relleno para el cálculo del volumen
a partir de las curvas de nivel o planos horizontales