Guía para el diseño… 05 Diseño de un relleno sanitario manual. Parte 4
..:: Una solución para la disposición final de
residuos sólidos municipales en pequeñas poblaciones ::..
OPS/CEPIS/PUB/02.93
Original: español
Jorge Jaramillo
Universidad de Antioquia, Colombia
|
|
Centro Panamericano de Ingeniería Sanitaria y Ciencias del Ambiente
División de Salud y Ambiente
Organización Panamericana de la Salud
Oficina Sanitaria Panamericana, Oficina Regional de la
Organización Mundial de la Salud
2002
5.6 Cálculo de la capacidad volumétrica del sitio8
La capacidad volumétrica del sitio es el volumen total disponible del terreno para recibir y almacenar la basura y el material de cobertura que conforman el relleno sanitario. En otras palabras, es el volumen comprendido entre la superficie de desplante y la superficie final del relleno, para lo cual es indispensable determinar la capacidad volumétrica del terreno.
En general, existen dos métodos para realizar este tipo de cálculo:
- Volúmenes de gran longitud y poca anchura.
- Volúmenes de gran extensión (extensos en ambas direcciones).
5.6.1 Volúmenes de gran longitud (alrededor de un eje)
Por lo general, el trabajo de campo en esta categoría de determinación de volúmenes comprende la obtención de secciones transversales a intervalos regulares a lo largo de un eje del proyecto (poligonal). Primero se calculan las áreas de estas secciones y luego, usando la regla de Simpson para volúmenes o la del prismoide, puede calcularse el volumen del material que se deberá retirar o colocar.
Método 1. Cálculo del volumen por la regla de Simpson
Una vez calculada el área de las distintas secciones, puede hallarse el volumen del material contenido en el corte o relleno por medio de la regla de Simpson, que es la misma que se emplea para las áreas, aunque las áreas de las secciones reemplazan a las ordenadas en la fórmula (figura 5.10 y apéndice D, ejemplo 5).
|
d
|
|||
| Volumen = |
—–
|
[A1 + A5 + 2 x A3 + 4(A2 + A4)]m3 |
[5-17]
|
|
3
|
Si llamamos M a la sección media, el volumen por la regla de Simpson será :
|
1
|
|||
| Volumen = |
—–
|
(d / 2)[A1 + A2’ + 2(cero) + 4 M] |
[5-18]
|
|
3
|
|
d
|
|||
| Volumen = |
—–
|
[A1 + A2 + 4M] |
[5-19]
|
|
6
|
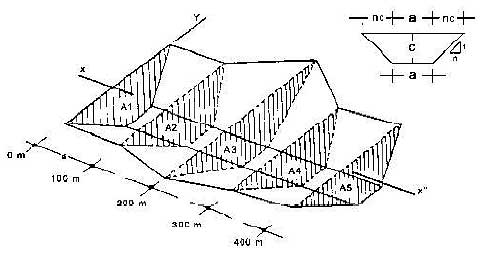 |
Figura 5.10
Volumen longitudinal alrededor de un eje
La ecuación [5-19] representa la regla del prismoide, que puede usarse para hallar el volumen de cualquier prismoide, siempre que se pueda conocer el área de la sección media (apéndice D, ejemplo 6).
Nota: el área M no es el promedio de las áreas A1 y A2.
Método 2. Cálculo del volumen por la regla del prismoide
El prismoide se define como un sólido que tiene dos caras planas y paralelas de forma regular o irregular, unidas por superficies planas o alabeadas, en las que se puedan trazar rectas desde una hasta la otra cara paralela. Algunos ejemplos de prismoides se presentan en la figura 5.11, cuya fórmula equivale a la [5-19].
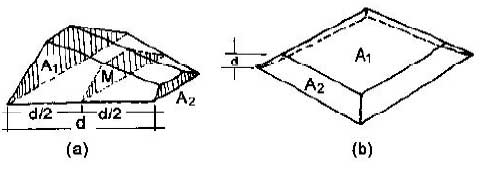 |
Figura 5.11
Prismoides
Para determinar su volumen por la regla de Simpson, es necesario dividir la figura de forma que resulte un número de secciones equidistantes; tres es el número menor que cumple esta condición.
Método 3. Volumen a partir de las áreas extremas
A partir del eje del proyecto y de la nivelación por franjas de un terreno, se puede calcular el volumen entre dos secciones transversales consecutivas, multiplicando el promedio de las áreas de las secciones por la distancia que las separa (para estar más cerca de la realidad, se recomienda tramos de 20 metros) (figura 5.12).
El volumen entre las secciones A1 y A2 está dado por:
|
(A1 + A2) x d 2
|
||
| Volumen = |
———————————
|
[5-20]
|
|
2
|
donde :
A1 + A2= Áreas de las secciones transversales (m2)
d = Distancia entre las secciones A1 y A2
Esta fórmula será más precisa a medida que A1 y A2 tiendan a ser iguales. En general, la precisión de este método es más que suficiente, puesto que se supone que el terreno será nivelado uniformemente entre las dos secciones, aunque se sabe que el volumen real es un tanto diferente (apéndice D, ejemplo 7).
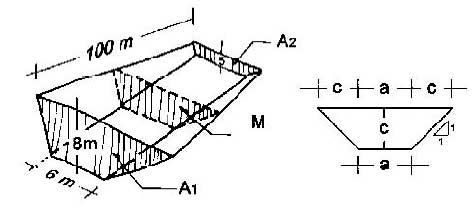 |
Figura 5.12
Volumen de un zanjón
5.6.2 Volúmenes de gran extensión
Método 1. De la retícula
Cuando se trata de hallar el volumen de un terreno de gran extensión y poca profundidad, el trabajo de campo consiste en cubrir el área de la superficie de desplante con una retícula de cuadros y obtener los niveles de sus vértices. El volumen total se puede calcular como la suma de volúmenes de todos los prismoides que tienen comoárea transversal un cuadro de la retícula y como altura la distancia a la superficie final del relleno. Esta altura estará dada por el promedio de las distancias entre la superficie de la configuración final del relleno y los vértices del cuadrado. Es decir, que si las elevaciones de los vértices de un cuadro son e1, e2, e3 y e4, la elevación de superficie final en este punto es ef, y el área de cada cuadrado de la retícula es A. Así, el volumen sería:
|
Vi = A (ef –(e1 + e2+ e3 + e4) / 4)
|
[5-21]
|
El grado de precisión que se obtenga será mayor mientras más pequeños sean los cuadrados de la retícula (apéndice D, ejemplo 8).
Método 2. A partir de las curvas de nivel
Consiste en determinar el volumen existente entre los planos horizontales del terreno, para lo cual es necesario calcular las áreas, luego promediarlas y multiplicarlas por la diferencia de altura que las separa. Se parte de la ecuación [5-20].
|
(A1 + A2)
|
||
|
V= |
——————————— ? ?h
|
[5-22]
|
|
2
|
Mientras más pequeño es el incremento ? ?h, mayor será la precisión del método. Además, será más fácil de usar si se tiene el levantamiento topográfico con curvas de nivel cada metro y si se utiliza un planímetro para el cálculo de las áreas. Este es el método más común en el caso de grandes rellenos sanitarios.
donde :
V = Volumen entre dos curvas de nivel (m3)
A1 + A2 = Áreas de los planos horizontales (m2)
? h = Diferencia de altura entre los planos (m)
Por tanto, la capacidad volumétrica del sitio está dada generalmente por la siguiente ecuación:
|
(A1 + A2)
|
(A2 + A3)
|
(A4 + A5)
|
||
|
V = |
———————– ? ?h1 +
|
——————– ? ?h2 +
|
———————— ? ?h3 +
|
[5-23]
|
|
2
|
2
|
2
|
Cuando las áreas tomadas son equidistantes entre sí:
|
? ?h
|
|||
|
V = |
—————-
|
A1 + 2 ?n-1 2 A1 + An |
[5-24]
|
|
2
|
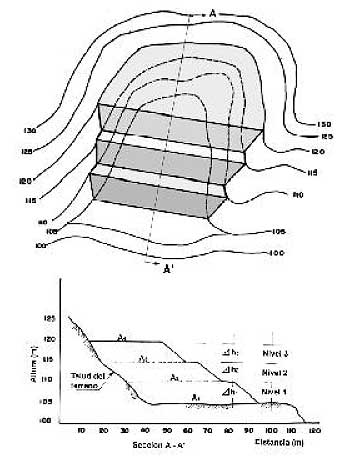 |
Figura 5.13
Planta y sección de un terreno
Cuando las curvas de nivel están muy separadas, si se desea obtener cierta precisión al calcular el volumen se puede emplear la fórmula del prismoide. Al aplicar esta fórmula se debe considerar que los planos de las curvas de nivel dividen la depresión en una serie de prismoides. El volumen de cada uno de ellos puede hallarse mediante aplicaciones sucesivas de la regla del prismoide o, en casos favorables, empleando directamente la regla de Simpson.
Al utilizar la fórmula del prismoide se toman las áreas de tres curvas a la vez y la del centro se usa como sección media. La precisión del resultado depende sobre todo de la diferencia de nivel entre las curvas. En general, a menor intervalo, mayor exactitud en el volumen.
5.7 Cálculo de la vida útil
El volumen del relleno —o sea, el volumen comprendido entre las configuraciones inicial y final del terreno, calculadas mediante cualquiera de los métodos descritos anteriormente— nos dará el volumen total disponible. El cuadro 5.3 facilita la recolección de esta información. El cálculo de la vida útil se puede estimar así: El volumen total disponible del terreno se compara con los valores del cuadro 5.1, columna 12 (donde aparecen los volúmenes acumulados del relleno) hasta encontrar un valor similar o ligeramente mayor. En la columna 0 de la misma línea se verá el número de años que equivalen a la vida útil del relleno.
5.8 Diseño del canal interceptor de aguas de escorrentía
Es importante estudiar la precipitación pluvial del lugar, con el fin de establecer las características de los drenajes perimetrales y las obras necesarias. Así se minimizará la producción del líquido lixiviado o percolado y se evitará la contaminación de las aguas.
Las aguas de lluvia que caen sobre las áreas vecinas al relleno sanitario suelen escurrirse hasta él, lo que dificulta la operación del relleno. Interceptar y desviar el escurrimiento de aguas de lluvia por medio de un canal perimetral fuera del relleno sanitario es, pues, un elemento fundamental de su infraestructura, que contribuirá a reducir el volumen del líquido percolado y mejorar las condiciones de operación. Es necesario construir un canal en tierra o suelo-cemento de forma trapezoidal y dimensionarlo teniendo en cuenta las condiciones de precipitación local, el área tributaria, las características del suelo, la vegetación y la pendiente del terreno (figuras 5.14 y 5.15).
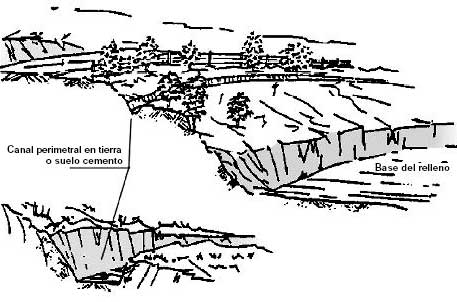 |
Figura 5.14
Drenaje perimetral para desviar las aguas de lluvia y red para lixiviado
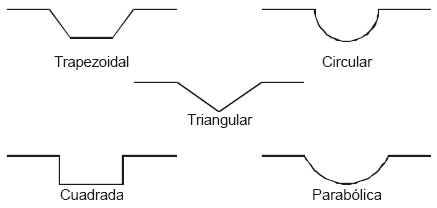 |
Figura 5.15
Tipos de sección de canales de drenaje de aguas de escorrentía
Para una pequeña cuenca se recomienda un canal con las dimensiones de la figura 5.16
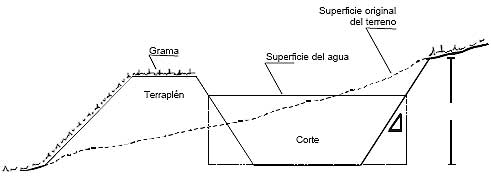 |
Figura 5.16
Detalle de la sección transversal del canal trapezoidal
Si por las características del lugar se requiere mayor precisión, se puede calcular el caudal que aporta la cuenca mediante el método racional y las dimensiones del canal según la siguiente fórmula.
|
Ki x Ad
|
||
|
Qp = |
—————-
|
[5-25]
|
|
3,6 x 106
|
donde:
Qp = Caudal que ingresa o máximo escurrimiento [m3/seg]
K = Coeficiente de escurrimiento.
i = Intensidad de la lluvia para una duración igual [mm/hora]
Ad = Área de la cuenca [m2]
tc = Tiempo de concentración [min]
El canal debe ser trazado por la curva de nivel más alta a la que llegará el borde del relleno sanitario y deberá garantizar una velocidad máxima promedio de 0,5 metros por segundo, que no provoque erosión excesiva; el tamaño de la sección del canal se podrá calcular usando la siguiente ecuación:
|
Qp
|
||
|
A = |
—————-
|
[5-26]
|
|
v
|
donde:
A = Área de la sección de la zanja [m2]
v = Velocidad máxima promedio [m/seg]
Una vez hallada el área de la sección, se deciden las dimensiones, sobre la base de las recomendaciones anteriores.
8 Tomado y adaptado de Irvine, Wiliam. Topografía. Áreas y volúmenes. McGraw-Hill. Capítulo 15. 1975.
