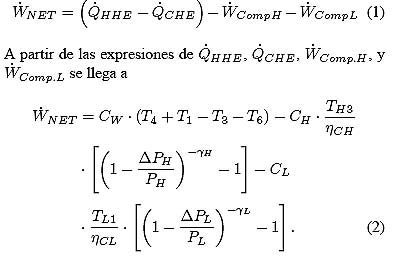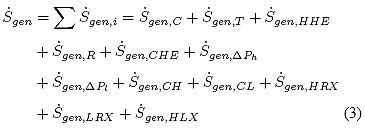Fugas de calor y aprovechamiento de efluentes en la optimización de ciclos Brayton totalmente irreversibles
En este trabajo se realiza optimización de máxima potencia y mínima generación de entropía sobre un modelo totalmente realista de un ciclo Brayton (máquinas irreversibles, flujos disipativos, consumo de potencia en todo trasiego de fluidos, transmisiones de calor a gradientes de temperatura finitos, fugas de calor, desaprovechamiento de efluentes, restricciones en caídas de presión y tamaño de intercambiadores). A manera de ejemplo se presenta un caso de estudio, en el cual, para unos parámetros de funcionamiento dados y variables dentro de rangos típicos, se determinan los conjuntos de valores optimizantes para las funciones objetivo, y se analiza la influencia de las fugas y del nivel de aprovechamiento de la exergía de los efluentes sobre estos conjuntos y sobre el comportamiento general del sistema. Los resultados obtenidos muestran comportamientos difícilmente predecibles. Este artículo ilustra un procedimiento implementable en computadora y que permite hacer evaluación de sistemas existentes y mejoramiento de diseños.
Descriptores: Ciclo Brayton irreversible; optimización termodinámica; exergía; mínima generación de entropía.
1. Introducción
La ingeniería tiene una importante meta en el campo de la termodinámica, la cual es mejorar el aprovechamiento de los recursos energéticos reduciendo la contaminación y produciendo más energía útil. Las fugas de calor y las corrientes de los efluentes constituyen pérdidas significativas de exergía si las primeras no se controlan y las segundas no se aprovechan efectivamente; además el desperdicio tiene implicaciones de carácter ambiental, porque obliga a un mayor uso del recurso combustible y aumenta la emisión de bióxido de carbono. Entre las acciones para controlar esta situación la comunidad científica está buscando fuentes de energía alternativa (celdas de combustible, eólica, solar y nuclear) y hace esfuerzos en mejorar los criterios de diseño de las plantas que empleen recursos fósiles para volverlas más amigables con el entorno y más eficientes energéticamente. Un paso importante en este último asunto es la modelación adecuada de los procesos, de tal manera que incluyan aspectos relevantes desde los puntos de vista energético y ecológico, cuestión que sólo se logra incorporando los efectos externos, esto es, análisis de sistemas extendidos.
Los ciclos de potencia han sido objeto de valiosas idealizaciones que fijaron pautas y guías para diseño, aunque las plantas se desvían de estas simplificaciones porque máquinas y procesos reales son imperfectos, y ensambles y arreglos no siguen fielmente los esquemas ideales. Por ejemplo, en el caso de los gases de combustión de calderas –asimilados a un reservorio de alta temperatura- su utilidad a la salida y sus implicaciones ecológicas deben incluirse en los análisis y diseños, reconociendo que la evacuación de estos gases a condiciones ambientales es una idealización susceptible de ser remodelada. Punto de suma importancia es aceptar que el trasiego de los fluidos fuente y sumidero consume una cantidad
de potencia mecánica que incide en la valoración termoeconmica del sistema y sus óptimos.
Modelar un sistema que trate de reproducir la realidad constituye reto para la ingeniería, siempre expuesta a controversias por las suposiciones y aproximaciones que los autores incorporan. El ciclo Brayton de potencia es un sistema típico convencional; sus estudios se han centrado en el ciclo en sí, dejando a un lado aspectos importantes de los alrededores inmediatos encubriendo efectos de las irreversibilidades relevantes desde el punto de vista de la calidad de la energía. El mejor modelo de sistema extendido se debe definir de tal manera que revele todas las irreversibilidades. En este trabajo se usa uno que satisface esas condiciones.
La optimización (que puede ser de carácter técnico, económico, ambiental, etcétera) tiene el propósito de encontrar el mejor arreglo y la mejor combinación posible de las condiciones de un sistema, asunto que en primer lugar implica identificar y definir un objetivo que se desee maximizar o minimizar, según sea el caso. Este propósito se expresa matemáticamente mediante la función objetivo, que puede ser, para el caso de plantas térmicas, maximizar la potencia producida, minimizar la entropía generada, maximizar la eficiencia exergética, minimizar el impacto ecológico, maximizar ganancias, o minimizar costos. Ya seleccionada la función objetivo, ésta debe expresarse como una ecuación en términos de variables y parámetros, y sujetarse a unas restricciones. Los parámetros son independientes de las variables y se consideran fijos en cada ejercicio particular. Las restricciones deben integrarse al modelo matemático mediante ecuaciones
adicionales a la función objetivo. Las variables pueden tomar distintos valores dentro de determinados rangos establecidos por su posibilidad física de alcanzar esos valores. Un proceso de optimización absoluta consistiría en calcular todos los valores de la función objetivo (el dominio) y encontrar el punto donde esa función es la mejor de todas: este valor es el óptimo absoluto. Lo anterior no sería muy interesante porque entrega un único resultado y no permite analizar el comportamiento de la función objetivo. Lo apropiado será entonces identificar y escoger una variable vital para el comportamiento del sistema y declararla “variable de decisión”, lo que permitirá visualizar las relaciones entre ella y la función objetivo. Cuando la variable de decisión tome un valor, cada una del resto de las variables podrá fluctuar dentro de sus respectivos rangos, esto causa que la función objetivo tome muchos valores; uno de estos valores es mejor que todos sus compañeros: se ha obtenido un óptimo local y un dominio local. En otras palabras, se han obtenido, para un valor de la variable de decisión, los valores que puede tomar la función objetivo y el mejor de ellos. Al conjunto de variables que entregan ese óptimo local se denomina aquí “Conjunto Optimizante”.
De acuerdo a todo lo anterior, si se examina el comportamiento de la función objetivo en todo el rango de la “variable de decisión”, se podrá encontrar el óptimo absoluto (óptimo entre óptimos). Se puede dar el caso en que la variable de decisión cause una respuesta monotónica en la función objetivo, esto es, que sólo la aumente o la disminuya, y por tanto no resultan puntos críticos (máximos o mínimos), luego en ese caso el mejor óptimo será el correspondiente al primero o al último del rango.
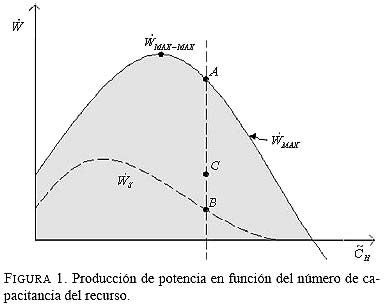
En el presente estudio se fijaron dos funciones objetivo: maximización de potencia neta producida y minimización de tasa de entropía generada. Para los dos casos se escogió la capacitancia térmica del fluido fuente de calor como variable de decisión. Esta capacitancia físicamente representa el insumo vital de la planta, se adimensiona como![]() , y se denomina número de capacitancia del recurso. Como se ilustra en las Figs. 1 y 2 (gráficas ejemplo), las zonas sombreadas corresponden a funcionamientos reales no optimizados y las curvas a sistemas optimizados. Es decir, para un valor
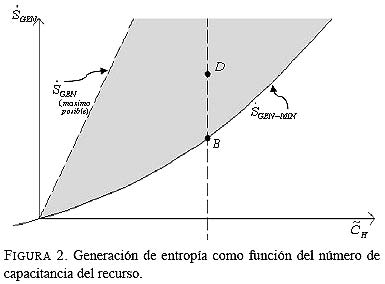
, y se denomina número de capacitancia del recurso. Como se ilustra en las Figs. 1 y 2 (gráficas ejemplo), las zonas sombreadas corresponden a funcionamientos reales no optimizados y las curvas a sistemas optimizados. Es decir, para un valor cualquiera, existe un conjunto de valores que dan el mejor rendimiento (máxima potencia o mínima entropía, puntos A y B); valores distintos entregan un sistema que produce menos potencia o genera más entropía (puntos C y D). Como se puede intuir, en una planta real la mínima generación de entropía
![]() es función monotónica creciente respecto del recurso y, como se aprecia en la Fig. 2, sólo será cero cuando la planta esté parada. Es además visible que existe un valor de
es función monotónica creciente respecto del recurso y, como se aprecia en la Fig. 2, sólo será cero cuando la planta esté parada. Es además visible que existe un valor de que produce más potencia que cualquier otro (MAX-MAX). Unos puntos muy interesantes son aquellos que indican la potencia neta evaluada a las condiciones de mínima generación de entropía (la curva a trazos Fig. 1, curva denominada
![]() ). Cada uno de esos puntos representa la potencia neta producida a un
). Cada uno de esos puntos representa la potencia neta producida a un dado y su correspondiente conjunto optimizante de generación de entropía, es decir, a mínimo nivel de irreversibilidades. En la Fig. 1 se representa con B, pues es el mismo punto B de la Fig. 2.
En la literatura técnica se pueden encontrar estudios de optimización del ciclo Brayton realizados desde diferentes enfoques y criterios, y con aproximaciones cada vez mas sofisticadas. Desde el ciclo Brayton ideal se pasó al endorreversible, y desde aquí se añadieron inter-enfriadores, regenerador, caídas de presión, reservorios de temperatura variables, etcétera. En este proceso evolutivo, la bibliografía sobre
|
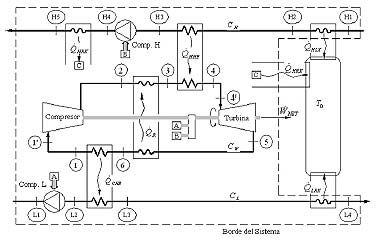
FIGURA 3. Esquema general de la planta [1]. H-corriente de alta temperatura (fuente), W- corriente de trabajo, L- corriente de baja temperatura (sumidero). Intercambiadores de calor reales: RRegenerador, HHE-intercambiador de alta, CHE- intercambiador de baja. Intercambiadores de calor virtuales: HRX- recuperador de alta, LRX- recuperador de baja, y HLX- intercambiador de fugas de |
tema ofrece optimizaciones de: potencia [2-6], tasa de generación de entropía [1,6-9], densidad de potencia [10-14], efi-
ciencia de primera ley [1,15,4,16], criterio ecológico [17-25], coeficiente de desempeño ecológico o ECOP [26,27], ganancia [28-30], y eficiencia de segunda ley [31-32]. Estas publicaciones hacen aproximaciones parciales: algunos incluyen regeneradores, inter-enfriadores, re-calentadores, irreversibilidades internas, caídas de presión en los intercambiadores y tuberías, o irreversibilidades externas por fugas de calor. Inclusive hay casos que consideran capacitancias térmicas finitas en la fuente y sumidero de calor. Por ejemplo, Chen et al. [33] optimizan un ciclo Brayton endorreveresible, regenerativo, con inter-enfriador y reservorios a temperatura variable. Revisiones generales del estado del arte pueden consultarse en la literatura técnica [34-36].
Efluentes y fugas de calor (objetos de este estudio) son componentes cuyos comportamientos deseables son triviales: aprovechar los primeros y reducir las segundas. En la realidad no es posible alcanzar una eliminación completa de las fugas, ni aprovechar totalmente los efluentes, pero estas situaciones sirven como puntos de referencia. Este trabajo no pretende extenderse sobre las citadas trivialidades, sino que profundizando la propuesta de la Ref. 1, al analizar el efecto
de los dos parámetros sobre los procesos de optimización de potencia neta y entropía generada, ofrece un conocimiento más realista que el de esa referencia. Beneficio de lo anterior es conocer (para dar un solo ejemplo) qué tanto se puede aumentar la potencia producida en una planta existente si
- Con el mismo
; se cambian el nivel de fugas y demás variables a valores optimizantes (buscando llegar al punto A).
- Con los mismos
y nivel de fugas; se cambian las variables a valores optimizantes.
- Con el mismo nivel de fugas; se cambian
y demás variables a valores optimizantes.
- Se cambian
, nivel de fugas y demás variables a valores optimizantes (buscando llegar al punto MAXMAX).
Desde la óptica de generación de entropía (mas no desde la de producción de potencia) el uso posterior de los efluentes es relevante. El concepto de sistema extendido es particularmenteútil en los criterios de optimización que impliquen calidad
de la energía. La cuantificación del desperdicio de esas corrientes usa el modelo de intercambiadores virtuales que se detallará posteriormente.
El sistema de estudio es un ciclo Brayton regenerativo cerrado. El modelo, representado en la Fig. 3, no hace ninguna concesión idealizante: el ciclo es irreversible tanto interna como externamente, todos los procesos de flujo son disipativos,
y todas las transferencias de calor son a diferencia finita de temperatura. La fuente y el sumidero, mostrados en las líneas remarcadas arriba y abajo, consisten en corrientes de gases a alta y baja temperaturas, que fluyen (consumiendo potencia) por intercambiadores donde transfieren calor a temperatura variable.
Aunque este artículo enseña resultados cuantitativos de un sólo caso de estudio, su pragmatismo radica en hacer difusión de un modelo realista y un método de análisis para su optimización, que pueden ser utilizados en diseños y evaluación de plantas. Esto es posible, pues al estar reportadas todas las ecuaciones, a partir de ellas y definiendo los parámetros particulares en cada caso, se puede realizar optimización con una herramienta computacional.
La contaminación producida en plantas se contabiliza en sus efluentes y se paga mediante impuestos o trueques por bonos o certificados. Estos pagos dependen de la cantidad de contaminante y de las tarifas aplicadas, que aunque educadas no dejan de ser arbitrarias. Una manera particularmenteútil para que el industrial sepa qué tanto está contaminando y qué tanto puede reducir esa contaminación, es mediante el cálculo de la generación de entropía y la comparación con la mínima entropía que su planta podría producir. El método expuesto en este trabajo pone al alcance esta herramienta, y también se puede convertir en criterio para establecer políticas energéticas.
2. Análisis teórico
2.1. Modelo
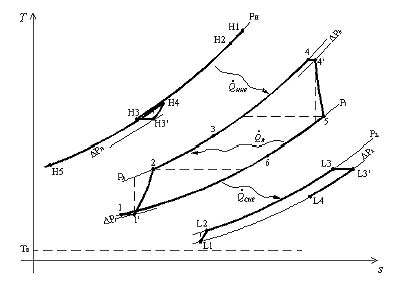
Este modelo (propuesto en la Ref. 1) se ilustra en la Fig. 3 y su correspondiente diagrama T-s, en la Fig. 4.
|
FIGURA 4. Diagrama T-s del sistema [1]. H-corriente fuente, L-corriente sumidero, h-lado de alta presión del ciclo; l- lado de baja presión del ciclo, _QR-calor transferido en regenerador, _QHHE- calor transferido desde la fuente, _QCHE- calor transferido hacia el sumidero. |
De esa referencia, la planta sigue un ciclo de potencia Brayton regenerativo 1-1’-2-3-4-4’-5-6-1, acoplado a una fuente de temperatura variable,TH y a un sumidero de temperatura variable,TL. El intercambiador de alta (HHE) permite la transferencia de energía entre la fuente y el fluido de trabajo. El intercambiador CHE permite el intercambio entre el ciclo y el sumidero. Las corrientes de alta, de trabajo y fría tienen capacitancias térmicas CH;CL y CW, respectivamente. Todos
los fluidos se tratan como gases ideales con calor específico constante y cambios de energía cinética y potencial despreciable.
Los intercambiadores y el regenerador R, se asumen de contracorriente para mínimas irreversibilidades. Se consideran caídas de presión,![]() , en los componentes de alta presión (tuberías, HHE y R), así como en el lado de baja presión; tanto
, en los componentes de alta presión (tuberías, HHE y R), así como en el lado de baja presión; tanto ![]() se manejan como expansiones isentálpicas [8] localizadas antes del compresor y turbina, respectivamente. También se consideran las caídas de presión
se manejan como expansiones isentálpicas [8] localizadas antes del compresor y turbina, respectivamente. También se consideran las caídas de presión ![]() en el fluido fuente y
en el fluido fuente y ![]() en el fluido sumidero.
en el fluido sumidero.
Las eficiencias isentrópicas de los compresores y turbina son ![]() . Los alrededores se asumen a To.
. Los alrededores se asumen a To.
La exergía de las corrientes de salida,![]() , puede aprovecharse en procesos externos o desperdiciarse descargándola directamente al ambiente sin ninguna recuperación. Según Ref. 1, la magnitud del desperdicio de exergía se incorpora mediante dos intercambiadores virtuales HRX y LRX, cuyos índices son
, puede aprovecharse en procesos externos o desperdiciarse descargándola directamente al ambiente sin ninguna recuperación. Según Ref. 1, la magnitud del desperdicio de exergía se incorpora mediante dos intercambiadores virtuales HRX y LRX, cuyos índices son, respectivamente.
Estos índices ficticios representan la relación entre la exergía desperdiciada y la disponible en la corriente que sale; un índice igual a uno indica descarga completa al ambiente con destrucción total de la exergía, y por el contrario, un índice igual a cero indica que hay recuperación completa. En consecuencia, es claro que dependen completamente de procesos externos. De manera similar están modeladas las pérdidas de calor desde los componentes del sistema: se incorporó un intercambiador virtual, HLX, ubicado aguas arriba del intercambiador de alta en el lado caliente. Estas pérdidas son expresadas como
![]() (exergía destruida sobre exergía disponible); típicamente se da valor de cero a  cuando se presupone que no hay pérdidas. Los índices de los tres intercambiadores virtuales se consideran como parámetros, es decir, valores conocidos y constantes. Este tratamiento es habilidoso en el sentido que permite integrar en un sólo análisis de optimización todos los procesos internos y externos, lo cual busca una mejor y sencilla aproximación con la realidad.
(exergía destruida sobre exergía disponible); típicamente se da valor de cero a  cuando se presupone que no hay pérdidas. Los índices de los tres intercambiadores virtuales se consideran como parámetros, es decir, valores conocidos y constantes. Este tratamiento es habilidoso en el sentido que permite integrar en un sólo análisis de optimización todos los procesos internos y externos, lo cual busca una mejor y sencilla aproximación con la realidad.
2.2. Potencia neta, generación de entropía y restricciones
La potencia neta del ciclo extendido es
|
|
Esta ecuación está en términos de las temperaturas intermedias del ciclo, pero se desea expresarla en función de los parámetros y variables. Para hacer esta transformación todas estas temperaturas se reescriben usando balances de primera y segunda ley en cada uno de los componentes. El detalle se encuentra disponible en la literatura [1].
La generación de entropía ![]() la suma de la tasas de generación de cada componente,
la suma de la tasas de generación de cada componente,![]() , que de acuerdo con
, que de acuerdo con
la Fig. 3 se puede expresar como
|
|
En forma análoga a generación de potencia, la Ec. (3) fue expresada [1] exclusivamente en términos de variables y parámetros.
El ciclo Brayton real está sometido a restricciones en el tamaño de los intercambiadores y pérdidas admisibles de presión. La restricción en el tamaño de intercambiadores significa una conductancia térmica total finita ![]() [8], que se puede repartir entre los intercambiadores y se expresa adimensionalmente mediante
[8], que se puede repartir entre los intercambiadores y se expresa adimensionalmente mediante ![]() donde
donde ![]() indica la fracción del área total disponible que está dedicada al intercambiador-i.
indica la fracción del área total disponible que está dedicada al intercambiador-i.
Si ![]() es la caída de presión admisible en el fluido0 de trabajo (de acuerdo a la Fig. 3,
es la caída de presión admisible en el fluido0 de trabajo (de acuerdo a la Fig. 3,![]() ), esta restricción puede expresarse adimensionalmente como
), esta restricción puede expresarse adimensionalmente como
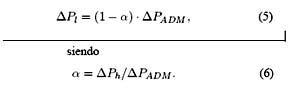 |
Con estas restricciones queda completamente definido el problema. Ahora las funciones objetivo pueden expresarse en términos de todos los parámetros, restricciones y variables de diseño adimensionadas. Estas funciones, además de trascendentes, son muy extensas y se expresan funcionalmente como
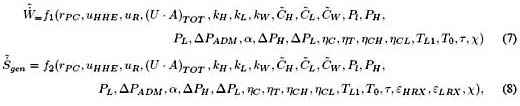 |
donde![]() es la potencia neta adimensional siendo
es la potencia neta adimensional siendo ![]() una potencia de referencia;
una potencia de referencia;![]() es generacón de entropía adimensional;
es generacón de entropía adimensional; ![]() es la relaci´on entre la temperatura de alta y de baja del ciclo;
es la relaci´on entre la temperatura de alta y de baja del ciclo; ![]() es el número de capacitancia donde
es el número de capacitancia donde![]() refieren las corrientes caliente, de trabajo, y fría, respectivamente.
refieren las corrientes caliente, de trabajo, y fría, respectivamente. ![]() Dado que la variable de decisión es
Dado que la variable de decisión es ;y fijando como parámetros
![]()
![]() entonces quedan como variables:
entonces quedan como variables: ![]()
Para que el lector desarrolle un proceso de optimización particular debe montar el sistema de ecuaciones (aquí descritos
y disponibles en la Ref. 1) en un computador con “software” de optimización matemática, y declarar los valores de los parámetros y los rangos de las variables.
3. Caso de estudio
Para ilustrar numéricamente el procedimiento propuesto se escogen los valores de parámetros y variables que se muestran en la Tabla I y la Tabla II.
Teniendo en cuenta que fugas de calor y desperdicio de efluentes son parámetros de operación, para poder observar sus efectos es necesario considerar diferentes valores de dichos parámetros. Este es, precisamente, el objeto de este trabajo.
El desperdicio en efluentes se supone igual en ambas salidas ![]() se examinan tres casos: 50, 75 y 100 %; también se examinan tres casos de magnitud de fugas x: 0, 10 y 20 %.
se examinan tres casos: 50, 75 y 100 %; también se examinan tres casos de magnitud de fugas x: 0, 10 y 20 %.
La solución de la función objetivo de máxima potencia produce un conjunto optimizante ![]() para cada
para cada , donde el subíndice
![]() especifica la pertenencia a la solución de máxima potencia.
especifica la pertenencia a la solución de máxima potencia.
 |
Es de notar que el desperdicio de los efluentes no afecta la potencia obtenida en el ciclo, lo cual está acorde con la Ec. (7), donde W aparece independiente de «. Alternativamente, la solución de la función objetivo de mínima generación de entropía produce un conjunto optimizante
 |
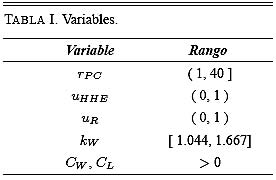
para cada ; donde el subíndice s especifica la pertenencia a la solución de mínima tasa de generación de entropía. La Fig. 5 ilustra el efecto de las fugas de calor(x) sobre la potencia máxima en función de
. Se observa, para un nivel de fugas dado, la existencia de un pico
que indica la máxima potencia entre todas las máximas. Es curioso ver que a partir de aquí, si se aumenta
, la potencia obtenida baja, y esto sólo se puede explicar mediante el argumento de que las potencias adicionales consumidas en trasiego de fluidos y en irreversibilidades superan el extra producido en la turbina. Por otra parte, comparando los tres valores
graficados, resulta que corresponden a diferentes
; además es visible que pasar de un nivel de fugas a otro mayor en un 10 %, implica disminución de la potencia obtenida en proporciones del orden de 20 %.
Desde el punto de vista práctico lo importante ahora es conocer los conjuntos optimizantes para cada , lo que implicaría seis gráficas; una por cada variable. Por razones de espacio y por relevancia, aquí sólo se reportan cuatro:
![]()
 |
 |
 |
 |
 |
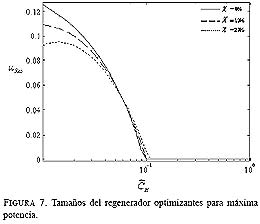
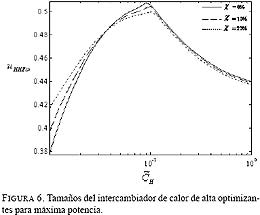
La Fig. 6 sólo muestra los valores del tamaño de intercambiador de alta![]() optimizantes. Según ella, esta variable no se ve muy afectada por el nivel de fugas presente.
optimizantes. Según ella, esta variable no se ve muy afectada por el nivel de fugas presente.
Aquí la cresta pronunciada no tiene relevancia ni influencia en el desempeño, y ocurre relativamente lejos del correspondiente a
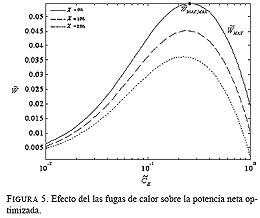
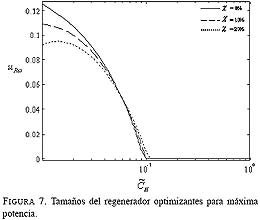
. La Fig. 7, complementaria con la Fig. 6 en el sentido de que entre las dos definen el tamaño de los tres intercambiadores reales, muestra que a partir de que
= 0:1 el regenerador no se justifica, independientemente del nivel de fugas.
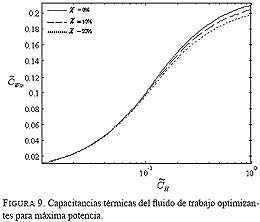
Las Figs. 8 y 9, importantes al mostrar el tamaño de las corrientes de los fluidos de enfriamiento y de trabajo que optimizan a , señalan que a mayores corrientes de fluido calefactor, mayores valores de ellos. En cuanto a las consecuencias de las fugas sobre las corrientes
![]() , se observa que a bajos
, se observa que a bajos no hay influencia.
 |
 |
 |
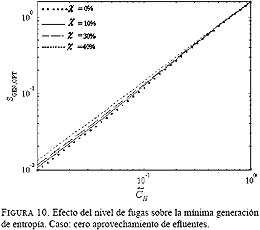
La función objetivo mínima generación de entropía se alcanza cuando se obtienen los conjuntos optimizantes s. La mínima generación de entropía, equivalente a la mínima destrucción de exergía, no es una curiosidad físico-matemática, sino un importante criterio ecológico natural. La Fig. 10 muestra el efecto de los distintos niveles de fugas de calor xsobre la mínima generación de entropía sin aprovechamiento de efluentes ( ![]() 100 %); como es de esperar, a mayor x mayor
100 %); como es de esperar, a mayor x mayor ![]() . El tope de generación de entropía por fugas ocurre -evidentemente- cuando se desperdicia todo el recurso, es decir, cuando el fluido fuente entrante se enfría por fugas hasta el estado de punto muerto; este es, además, el tope de generación de entropía absoluto, pues no se puede concebir una situación peor. La cuantificación de la generación de entropía en este caso se hace mediante la Ec. (9) haciendo
. El tope de generación de entropía por fugas ocurre -evidentemente- cuando se desperdicia todo el recurso, es decir, cuando el fluido fuente entrante se enfría por fugas hasta el estado de punto muerto; este es, además, el tope de generación de entropía absoluto, pues no se puede concebir una situación peor. La cuantificación de la generación de entropía en este caso se hace mediante la Ec. (9) haciendo ![]()
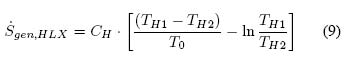 |
Como se ha insistido, el beneficio práctico que entrega este análisis es, para un nivel de fugas dado, conocer la mínima generación de entropía, y el conjunto de valores optimizantes correspondiente; operar la planta a valores distintos conducirá a mayor generación de entropía.
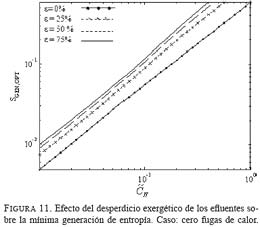
La Fig. 11 ilustra la mínima generación de entropía a diferentes niveles de aprovechamiento de efluentes para cero fugas de calor. Como en el caso anterior, a partir de ella se aprecia el mejor comportamiento posible para cada , además, es base para encontrar el conjunto optimizante, y permite comparación del nivel actual de generación de entropía en un diseño o de una planta versus el mínimo deseable.
Siguiendo un procedimiento análogo al utilizado en producción de potencia se pueden determinar los conjuntos optimizantes.
El desempeño de máquinas reales también se puede caracterizar mediante las curvas potencia versus eficiencia térmica, que típicamente presentan rizos debido a que los puntos de máxima potencia y máxima eficiencia son distintos [12,37-39].
Para analizar la influencia de las fugas y del aprovechamiento de efluentes en el comportamiento de estos rizos se selecciona un (0.071) con sus correspondientes conjunto optimizante y
la variación de Wse consigue liberando la relación de compresión
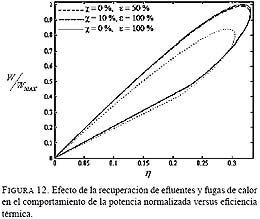
![]() . Según la Fig. 12 el aprovechamiento de efluentes no tiene relevancia, asunto que se explica en el hecho de que tal ocurrencia es externa al sistema. La comparación de los rizos correspondientes a distintas fugas también entrega un resultado esperado: potencias y eficiencias se reducen sensiblemente en la medida en que el nivel de fugas aumenta. En este caso particular un aumento del 0 al 10% en las fugas se traduce en disminución de la potencia máxima de 20 %, mientras que la eficiencia máxima se reduce de 35 a 31 %.
. Según la Fig. 12 el aprovechamiento de efluentes no tiene relevancia, asunto que se explica en el hecho de que tal ocurrencia es externa al sistema. La comparación de los rizos correspondientes a distintas fugas también entrega un resultado esperado: potencias y eficiencias se reducen sensiblemente en la medida en que el nivel de fugas aumenta. En este caso particular un aumento del 0 al 10% en las fugas se traduce en disminución de la potencia máxima de 20 %, mientras que la eficiencia máxima se reduce de 35 a 31 %.
 |
4. Conclusiones
A partir del modelo usado (que no hace concesiones en reversibilidades ni pérdidas y que contabiliza todas las potencias para trasiego de fluidos) se logra un análisis de optimización de aplicación práctica.
El procedimiento ilustrado puede adaptarse para explorar los efectos de otros parámetros en producción de potencia y generación de entropía. Esto puede ser aprovechado tanto por un diseñador como por un operador de planta.
A partir del conocimiento del punto de operación óptimo se puede juzgar el desempeño de una planta, y también cuantificar las desviaciones de las distintas condiciones de operación respecto de las optimizantes.
Para un caso de estudio se identificó la influencia de las fugas y del nivel de desperdicio exergético de efluentes en la optimización. Se encontró que cada conjunto optimizante depende del nivel de fugas tanto maximizando potencia obtenida como minimizando entropía generada.
El método expuesto, permite, para una potencia dada, encontrar el mejor punto de operación desde el punto de vista ecológico: el de mínima generación de entropía.
Queda ilustrado un procedimiento implementable en computador y que permite hacer evaluación de sistemas existentes, y mejoramiento de diseños.
Agradecimientos
Los autores presentan especial agradecimiento a la Universidad del Valle por el apoyo financiero dado a través del proyecto No CI-2451.
————————————————————————————————————————————————–
- C.A. Herrera, J. Sandoval y M. Rosillo, J. Phys. D: Appl. Phys 39 (2006) 3414.
- . J. Chen, J. Phys. D: Appl. Phys 27 (1994) 1144.
- C.Y. Cheng y C.K. Chen Energy 21 (1996) 241.
- S. ¨ Ozkaynak, S. G¨oktun y H. Yavuz, J. Phys. D: Appl. Phys 27 (1994) 1139.
- G. Aragón-González, A. Canales-Palma y A. León-Galicia, J. Phys. D: Appl. Phys 33 (2000) 1403.
- P. Salamon, K.H. Hoffmann, S. Schubert, R.S. Berry y B. Andresen, J. Non-Equilib. Thermodyn. 26 (2001) 73.
- A. Bejan, Entropy generation through heat and fluid flow (New York: John Wiley and Sons Inc., 1982).
- A. Bejan, Entropy generation minimization (New York: CRC Press, 1996).
- A. Bejan, Advanced engineering thermodynamics, 2nd ed. (New York: John Wiley and Sons Inc., 1997).
- B. Sahin, A. Kodal y H. Yavuz, J. Phys. D: Appl. Phys 28 (1995) 1309.
- B. Sahin, A. Kodal, T. Yilmaz y H. Yavuz, J. Phys. D: Appl. Phys 29 (1996) 1162.
- L. Chen, J. Zheng, F. Sun y C. Wu, J. Phys. D: Appl. Phys 34 (2001a) 1727.
- L. Chen, J. Zheng, F. Sun y C. Wu, J. Phys. D: Appl. Phys 34 (2001b) 422.
- L. Chen, J. Zheng, F. Sun y C. Wu, Exergy an International Journal 2 (2002) 345.
- J.M.M. Rocco, S. Velasco, A. Medina y A. Calvo Hernandez, J. Appl. Phys. 82 (1997) 2735.
- G. Aragón-González, A. Canales-Palma, A. Leon-Galicia y M. Mucharrafie-Martinez, J. Phys. D: Appl. Phys 36 (2003) 280.
- F. Angulo-Brown, J. Appl. Phys. 69 (1991) 7465.
- Z. Yan, J. Appl. Phys. 73 (1993) 3583.
- C.Y. Cheng y C.K. Chen, J. Phys. D: Appl. Phys 30 (1997) 1602.
- C.Y. Cheng y C.K. Chen, Energy Convers. Manage. 39 (1998) 33.
- C.Y. Cheng y C.K. Chen, J. Phys. D: Appl. Phys 32 (1999) 350.
- F. Angulo-Brown, L. Arias-Hernandez y R.A. Paez-Hernandez, J. Phys. D: Appl. Phys 32 (1999) 1415.
- F. Angulo-Brown, G. Ares de Parga y L.A. Arias-Hernandez, J. Phys. D: Appl. Phys 35 (2002) 1089.
- Y.C. Huang, C.I. Hung y C.K. Chen, En: CSME Proceedings of the 14th National Conference on Mechanical Engineering, Taiwan (1997) 288.
- Y. Ust, A. Safa y B. Sahin Appl. Energ. 80 (2005) 247.
- Y. Ust, B. Sahin, A. Kodal y I. Hakki Akcay, Appl. Energ. 83 (2006a) 558.
- Y. Ust, B. Sahin y A. Kodal, Int J Therm Sci 45 (2006b) 94.
- P. Salamon, R.S. Berry y G. Heal, Resour Energ 1 (1978) 125.
- P. Salamon y A. Nitza J Chem Phys 74 (1981) 3546.
- L. Chen, F. Sun y C. Wu, Appl Energ 79 (2004) 15.
- J.B. Woodward, J Energ Resour-Asme 117 (1995) 343.
- C.K. Chen y Y.F. Su, Int J Therm Sci Sciences 44 (2005) 303.
- L. Chen, W. Wang, F. Sun y C. Wu, Peformance of a variabletemperature heat reservoirs endoreversible closed intercooled regenerated Brayton cycle. Cap. 15 en L. Chen, F. Sun editors. Advances in finite-time thermodynamics. New York: Nova Science Publishers. 2004
- L. Chen, C.Wu y F. Sun J. Non-Equilib. Thermodyn. 24 (1999) 327.
- A. Durmayaz, O. Salim Sogut, B. Sahin y H. Yavuz, Prog Energ Combust 30 (2004) 175.
- L. Chen y F. Sun, editors. Advances in finite-time thermodynamics (New York: Nova Science Publishers, 2004).
- J.M. Gordon, Am. J. Phys. 59 (1991) 551.
- G. Aragón-González, A. Canales-Palma y A. León-Galicia, J. Phys. D: Appl. Phys 33 (2000) 1403.
- J.M. Gordon y M. Huleihil, Am. J. Phys. 72 (1992) 829. Rev. Mex. Fís. 54 (2) (2008) 118–126
Por: C.A. Herrera, M.E. Rosillo y L. Castaño
Escuela de Ingeniería Mecánica, Universidad del Valle,
A.A. 25 360, Cali – Colombia,
Fuente: Revista mexicana de Física