Caracterización morfométrica de la cuenca alta del río Sauce Grande, Buenos Aires, Argentina

RESUMEN

La cuenca alta del río Sauce Grande abastece el complejo hidráulico Embalse Paso de las Piedras, comportándose como servicio ambiental primordial para el consumo hídrico de Bahía Blanca. El análisis de las características morfométricas y funcionales de una cuenca hidrográfica a través de parámetros de forma, relieve y red de drenaje, es básico en la modelación hidrológica para determinar el movimiento y captación del agua de lluvia. Estos indicadores pueden apoyar una formulación de un Sistema de Pago por Servicios Ambientales, como estrategia básica de ordenamiento territorial y desarrollo local, centrado en la oferta de agua generada por la cuenca. El objetivo fue caracterizar morfométricamente la cuenca alta del río Sauce Grande. La metodología aplicada se basó en establecer y analizar los parámetros morfométricos mediante el uso de Sistemas de Información Geográfica y planillas de cálculo, a partir de un modelo digital del terreno e imágenes satelitales. Los resultados alcanzados definieron que la cuenca posee un área de 1502.6 km2. La longitud axial es de 41.6 km con un ancho promedio de 36.1 km. El Factor de forma (0.87) indica que posee forma alargada, siendo rectangular oblonga según el coeficiente de compacidad de Gravelius (2.8).

La longitud del cauce principal es 58.34 km con pendiente media de 0.48 %. La densidad de drenaje es 0.27 km.km-2 y su coeficiente de sinuosidad 1.42. El tiempo de concentración es 11.8 hs. La curva hipsométrica adimensional corresponde a una cuenca con un avanzado grado de desarrollo. Todos estos parámetros facilitan la cuantificación del caudal líquido en la cuenca.

INTRODUCCIÓN

El funcionamiento de una cuenca se asemeja al de un colector que recibe la precipitación y convirtiendo parte de esta en escurrimiento. La transformación depende de las condiciones climáticas y las características físicas de la cuenca.
Desde el punto de vista de su funcionamiento, una cuenca hidrográfica puede caracterizarse por su morfología, por la naturaleza del suelo y por la cobertura vegetal y uso del suelo (Henaos, 1988; Mintegui Aguirre & López Unzú, 1990; Gaspari, 2002; Gaspari et al., 2009).

La influencia de estos factores sobre la transformación de la precipitación en escurrimiento es fácilmente predecible cualitativamente, estribando la dificultad en expresar estas influencias mediante parámetros sencillos. Sin embargo, es posible definir cierto número de índices, susceptibles de servir, al menos de referencia, en la clasificación de cuencas y de facilitar los estudios de semejanza (López Cadenas de Llano, 1998).

Las propiedades morfométricas de una cuenca hidrográfica proporcionan una descripción física espacial que permite realizar comparaciones entre distintas cuencas hidrográficas. Al mismo tiempo, pueden proporcionar conclusiones preliminares sobre las características ambientales del territorio a partir de la descripción precisa de la geometría de las formas superficiales.

La morfometría particular de cada cuenca hidrográfica, ante eventos climáticos, esta relacionada con la posibilidad de aprovechamiento hídrico y con la generación de una respuesta a los mismos, como la escorrentía superficial expresada
en términos de caudales, la incidencia en el transporte de sedimentos y nutrientes a lo largo de los ecosistemas que la integran.

En la actualidad, herramientas metodológicas tales como los Sistemas de Información Geográfica (SIG) y la interpretación de imágenes satelitales, permiten realizar la caracterización espacio temporal de las propiedades morfométricas de las cuencas hídricas y de las redes de drenaje.

El análisis de las características morfométricas y funcionales de una cuenca hidrográfica a través de parámetros de forma, relieve y red de drenaje, es básico en la modelación hidrológica para determinar el movimiento y captación del agua de lluvia (Gaspari et al, 2009). Asimismo, esta modelación permite explicar el movimiento del agua superficial y predefinir la oferta hídrica complementada con otros modelos matemáticos. Esta oferta de agua puede ser el inicio de una estrategia básica de ordenamiento territorial y desarrollo local, representada por un Sistema de Pago por Servicios Ambientales (PSA). El PSA es un instrumento para lograr una asignación eficiente de los recursos naturales concentrándose en los servicios hídricos, la disponibilidad y calidad del agua.

El PSA se considera una posible solución para financiar la conservación del recurso hídrico y el ambiente en la cuenca alta del río Sauce Grande.

El objetivo del trabajo fue caracterizar morfométricamente la cuenca alta del río Sauce Grande, como material de apoyo al PSA.

MATERIALES Y MÉTODOS

La cuenca hidrográfica es una unidad espacial compuesta de una gran diversidad de componentes bióticos y abióticos que interactúan entre sí.

Los parámetros morfométricos de una cuenca hidrográfica serrana, desempeñan un papel fundamental en el estudio y comportamiento en los componentes del ciclo hidrológico. Asimismo, algunos parámetros son requeridos como datos de entrada en la mayoría de los modelos hidrológicos para el análisis de las características morfológicas y funcionales, para un potencial ordenamiento territorial.

El marco espacial del presente estudio fue la cuenca alta del río Sauce Grande, situada en el sudoeste bonaerense, Argentina (Figura 1). La misma abastece el complejo hidráulico Embalse Paso de las Piedras, comportándose como servicio ambiental primordial para el consumo hídrico de Bahía Blanca.

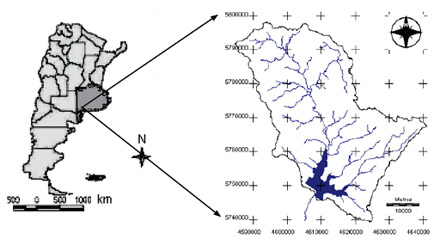Figura 1. Mapa de ubicación de la cuenca alta del río Sauce Grande, Provincia de Buenos Aires, Argentina.

La cuenca alta del río Sauce Grande (CARSG) (Provincia de Buenos Aires), se encuentra ubicada en el contexto geológico de las Sierras Australes. Presenta tres unidades geomorfológicas importantes: las serranías, los niveles de piedemonte con cobertura loéssica y el valle del río (Rabassa, 1982).

La primera incluye al cordón de Ventania, Las Tunas y Pillahuincó con pendientes pronunciadas en la zona de divisoria de aguas. En esa zona se observan cárcavas de carácter torrencial que dan lugar a la formación de la mayoría de los afluentes, algunos permanentes y otros temporarios, que discurren en pequeños y profundos cañadones sobre las pendientes más pronunciadas. Posteriormente, se presenta la zona del pedemonte, que alcanza a áreas de menores pendientes. Por último, la unidad geomorfológica correspondiente a la llanura aluvial del río, compuesta principalmente por material sedimentario moderno con un espesor variable y pendientes más moderadas. Se destaca la presencia de barrancas (escarpas de erosión) cuyas paredes verticales y alturas variables (entre 3 y 8 m) encajonan y controlan el cauce del río (Luque et al., 1979).

Las unidades cartográficas de suelos de la cuenca corresponden a los “Dominios edáficos” 1, 2 y 3 del Mapa de Suelos del INTA (INTA, 1989). Cada uno de ellos está representado por diversas unidades taxonómicas, las que permiten expresar la potencialidad productiva de los suelos.

Están desarrolladas sobre material loéssico que ha cubierto totalmente el faldeo de las sierras. Algunos suelos han evolucionado a partir de sedimentos arenosos apoyados sobre calcretas (tosca). Las pendientes y senos entre lomas están ocupadas por Argiudoles típicos inclinados, en las partes distales del pedemonte, con predominio de pastizales naturales. Donde el relieve se atenúa, se hallan Argiudoles típicos de familia fina, someros, con uso del suelo ganadero-agrícola.

En la parte superior de las lomas, donde las calcretas están más cercana a la superficie, se desarrollan Hapludoles petrocálcicos, con ganadería extensiva. En las vías de escurrimiento que nacen en los faldeos y luego ingresan en otras unidades geomorfológicas se hallan Haplustoles típico, éntico y lítico, donde la actividad principal se expresa con una combinación de agricultura y ganadería (Gaspari, 2002).

El análisis de las características morfológicas y funcionales de la cuenca alta del río Sauce Grande, se basó en establecer y analizar los parámetros morfométricos de forma, de relieve y relativos a la red hidrográfica, mediante el uso de Sistemas de Información Geográfica (SIG) Idrisi Taiga ® (Eastman, 2006) y planillas de cálculo. Además se enriqueció el trabajo con un análisis general topográfico de manera de integrar el relieve y el propio trazado de los ríos. Es un concepto fundamental en el análisis de la hidrografía, en especial, en el estudio de las aguas continentales.

El material de base utilizado fue cartografía topográfica del Instituto Geográfico Militar (IGM), a escala 1:50.000, denominadas Tornquist, Sierra de la Ventana, Peralta, Tres Picos, Saldungaray, Estancia Las Águilas, Cabildo y Lartigau. Además se emplearon imágenes satelitales Landsat 5, 226/086 y 226/087 con fecha 26 de marzo de 2003, obtenidas en la Comisión Nacional de Actividades Espaciales (CONAE), y el modelo digital de elevación del Misión Shuttle Radar Topography Mission (SRTM) en formato ASCII, disponible en la web gratuitamente bajo entorno Google Earth ©, el cual representa el modelo digital de elevación de la superficie terrestre de buena resolución espacial. Este mapa fue recortado al área de estudio para su posterior procesamiento con el SIG.

La red de drenaje fue creada por digitalización en pantalla a partir de una composición de las bandas 1, 2 y 3 del satélite Landsat 5, anteriormente mencionado, y con apoyo de imágenes actuales disponibles en Google Earth ©.

Desde el punto de vista hidrológico, cuenca hidrográfica se define como el territorio que ocupa el río principal y sus afluentes, cuyos límites son definidos por la topografía del terreno a partir de las divisorias de aguas. La delimitación de la cuenca alta del río Sauce Grande se realizó por divisoria de aguas sobre cartografía topográfica.

Posteriormente, se corroboró con un procesamiento automático con SIG sobre el modelo de elevación digital SRTM.

El cauce o lecho de un río es el canal natural por el que circulan las aguas generadas dentro de la cuenca hidrográfica. En un análisis integrador de la superficie de la CARSG con su cauce (laderas), intervienen dos conceptos: perfil transversal y el longitudinal de la cuenca. El transversal representa el perfil que indicaría el fondo del cauce y la divisoria topográfica hacia ambos lados, indicando una depresión cóncava con la parte más profunda donde circula el río.
El perfil longitudinal indica el talweg desde la divisoria de agua de la cuenca hasta su desembocadura. Además, describe la forma en el que éste varía su cota a lo largo de su longitud y recorrido; de tal modo que refleja la pendiente de cada tramo, determinada por las condiciones impuestas por el tramo aguas arriba. La representación gráfica expresa la capacidad erosiva del río por medio de la relación entre la distancia recorrida desde su nacimiento y la altura
relativa de cada punto de dicho perfil. Cabe mencionar que el perfil longitudinal y el mapa topográfico son descripciones continuas de la superficie.

La gráfica de los perfiles mencionados se realizó a partir de la digitalización en pantalla de una polilínea, para cada perfil, que contiene sus extremos sobre el modelo de elevación digital y en coincidencia con el límite de la CARSG. Para ello se utilizó un módulo del SIG, el cual genera un perfil (línea continua) que muestra los valores de cada uno de los píxeles que cruza. En el caso del perfil transversal se realizaron tres cortes caracterizando las grandes morfologías que
presenta la cuenca: cuenca alta, media y baja. El perfil longitudinal tomó como base una línea recta paralela a la red de drenaje principal.

Otros indicadores destinados a determinar la influencia de la forma de la cuenca en el movimiento y captación del agua de lluvia, se engloban en los parámetros de forma, relieve y de la red de drenaje (López Cadenas del Llano, 1998). La determinación de estos parámetros se realizó a nivel de cuenca hidrográfica según las metodologías mencionadas a continuación:

Parámetros de Forma

Perímetro (P) (km): Es la medición de la línea envolvente de la cuenca hidrográfica, a lo largo de la divisoria de aguas topográficas.

Longitud Axial (La) (km): Es la distancia existente entre la desembocadura y el punto más lejano de la cuenca. Es el mismo eje de la cuenca (Henaos, 1988). Es la longitud de la línea recta que conecta los puntos extremos de la cuenca en forma aproximadamente paralela al curso principal (Morisawa, 1959).

Longitud del curso principal (L) (m): Es la longitud del río desde el punto más distante de la cuenca hasta la desembocadura.

Longitud total del drenaje (Ln) (km): Es la longitud definida con la sumatoria de las longitudes de todos los cursos de agua que drenan por la cuenca

Coeficiente de sinuosidad total (S): Es la relación entre la longitud del río principal a lo largo de su cauce (L) y la longitud en línea curva o recta entre el inicio y final del cauce (Ld). Es un coeficiente adimensional (Llamas, 1993).

Área (A) (km2): Es la superficie encerrada por la divisoria de aguas.

Ancho promedio (Ap) (km): Es la relación entre la superficie de la cuenca por su longitud axial (La).

Factor de forma (IF): Es un factor adimensional que indica como se regula la concentración del escurrimiento superficial
en la cuenca hidrográfica. Se expresa como la relación entre el ancho promedio de la cuenca y su longitud axial (Jardí, 1985; Henaos, 1988). Manifiesta la tendencia de la cuenca hacia las crecidas. Cuando IF es similar a 1, representa una cuenca de forma redondeada. La cuenca con IF bajo, se caracteriza por ser una cuenca alargada, y son menos propensas a tener lluvias intensas y simultáneas sobre su superficie y estará sujeta a crecientes de menor magnitud, que un área de igual tamaño con un factor de forma mayor (Henaos, 1988). Una cuenca de forma triangular, con dos vértices en las cabeceras, afluentes de similar longitud y sincronismo en la llegada, provocará crecidas más significativas.

Coeficiente de compacidad de Gravelius (Kc): Este parámetro es adimensional y relaciona el perímetro de la cuenca con el perímetro de un círculo teórico de área equivalente al de la cuenca (Gaspari, 2002).

El círculo teórico representa un límite que define la forma y la superficie que abarca la cuenca vertiente, teniendo influencia sobre los escurrimientos y sobre la marcha del hidrograma resultante de una precipitación (López Cadenas de Llano & Mintegui Aguirre, 1987).

Para explicar el Kc de una cuenca, se ha propuesto su comparación con una cuenca ideal de forma circular, con sus tributarios dispuestos radialmente y que desembocan en el punto central (López Cadenas de Llano, 1998). Se expresa como una relación entre el perímetro (P (km)) y su superficie (A (km2)), por medio de la Ecuación 1.

Kc = P / (2 √ Π x A) (Ecuación 1)

El Kc está relacionado estrechamente con el tiempo de concentración, que es el tiempo que tarda una gota de lluvia en moverse desde la parte más lejana de la cuenca hasta la salida. En este momento ocurre la máxima concentración de agua, puesto que están llegando las gotas de lluvia de todos los puntos de la cuenca. Según el valor que tome este coeficiente, la cuenca tendrá diferente forma: Kc = 1.00 representa una cuenca redonda; Kc = 1.25, oval redonda;
Kc = 1.50 oblonga; Kc igual o mayor a 1.75 indica una cuenca rectangular-oblonga. Su valor será mayor que la unidad y crecerá con la irregularidad de la forma de la cuenca. A medida que su Kc tiende a 1, es decir cuando tiende a ser redonda, la peligrosidad de la cuenca a las crecidas es mayor, porque las distancias relativas de los puntos de la divisoria con respecto a uno central, no presenta diferencias mayores y el tiempo de concentración se hace menor,
por lo tanto mayor será la posibilidad de que las ondas de crecidas sean continuas.

Parámetros de Relieve

Curva hipsométrica adimensional (CHA).
Expresa el potencial evolutivo de la cuenca hidrográfica, por medio de un gráfico de dos ejes, donde la ordenada representa la Altura relativa (h/H) y la abscisa el Área relativa (a/A), donde h: Intervalo entre curvas de nivel (m), H: Desnivel total de la cuenca (m), A: Superficie total de la cuenca (ha) y a: Área entre curvas de nivel (ha). Su forma es sigmoidal, cóncava hacia arriba en la parte superior y convexa en la parte baja. El grado de sinuosidad es muy variable, igual que la pendiente enel punto de inflexión. Cuando las curvas hipsométricas presentan variaciones, ya sea por apartarse de las teóricas o por presentar más de un punto de inflexión, puede relacionarse con controles tectónicos o litológicos particulares (Racca, 2007). La CHA se determinó con apoyo en el modelo digital de elevación con un SIG, a intervalos altimétricos de diez metros y su relación a la superficie de ocupación.

Además se estableció la integral hipsométrica que representa el valor del área relativa que yace sobre y bajo la curva. Estos datos están disponibles en la base de datos digital de la cátedra de Manejo de Cuencas Hidrográficas ([email protected]).

Pendiente media de la cuenca (PM): El proceso de degradación a que se ve sometida una cuenca hidrográfica, al igual que el caudal máximo, están muy influenciados por la configuración topográfica, debido a que el poder erosivo se manifiesta en mayor o menor grado de acuerdo a los distintos grados de pendiente (Henaos, 1988; López Cadenas de Llano, 1998).

Para determinar la pendiente media (PM) de la cuenca se utilizó el mapa topográfico, con aplicación del SIG, como se expresa en la Ecuación 2.

PM = 100 [(H x L) / A] (Ecuación 2)

Siendo PM: Pendiente media (%); H: Distancia vertical entre curvas medidas (equidistancia) (km); L: Longitud total de las curvas de nivel (km); A: Superficie (km2).

A partir del mapa topográfico y con apoyo en el SRTM, se generó un modelo digital de elevación (MDE), a partir del cual se realizó un mapa de pendientes (en %). Según la clasificación de pendiente (en %) de López Cadenas de Llano (1998), se representaron cartográficamente los diferentes tipos de relieve: muy plano a un relieve menor del 0.5 %; plano a 0.5 a 1 %, de 1 a 3 % suave; de 3 a 12 % presenta lomadas; 12 a 20 % relieve accidentado; 20 a 50% muy fuerte; escarpado cuando se distribuye entre 50 y 75 %, y mayor al 75 % se corresponde a un relieve muy escarpado.

Coeficiente de rugosidad (Ra): Es la relación existente entre el desnivel de la cuenca (H) y su densidad de drenaje (Dd). Es adimensional (Gaspari et al., 2009). Patton (1988) menciona que cuencas muy disectadas con bajo relieve presentan un Ra similar a cuencas moderadamente disectadas y con un alto relieve. Orientación de ladera: Llamas (1993) expresa que es la dirección geográfica con respecto al norte geográfico, según la resultante de la pendiente general de las laderas de la cuenca. Su análisis se realizó en un mapa que indica la orientación con SIG sobre el modelo digital de elevación.

Parámetros de Drenaje

Clasificación de la red de drenaje según Strahler. Se utilizó el esquema de ordenación o de clasificación de Horton-Strahler, el cual expresa que las redes de drenaje pueden ser modeladas o representadas por un conjunto de nodos conectados unos a otros por segmentos, de manera que cada nodo tiene solo una ruta hacia la salida (Strahler, 1964). Según Strahler (l.c.) una corriente puede tener uno o más segmentos, siendo un canal una unión arbitraria de segmentos.

Para jerarquizar una red de drenaje se asignan valores numéricos a los órdenes de los cursos que conforman la red de drenaje, asignándole valor 1 a los cursos que son las nacientes, valor 2 a la conjunción de dos cauces de orden 1, valor 3 a la unión entre dos cauces de orden 2. Así se procede sucesivamente hasta finalizar con la jerarquización de la red de drenaje. El curso de agua cuyo cauce alcanza la máxima magnitud dentro del área ocupada por la cuenca, es el río principal.

Densidad de drenaje (Dd): Está definida para cada cuenca como la relación entre la suma de las longitudes de todos los cursos de agua que drenan por la cuenca con respecto al área de la misma (López Cadenas de Llano y Mintegui Aguirre, 1987; López Cadenas de Llano, 1998). Dd caracteriza cuantitativamente la red hidrográfica de la cuenca, por medio del grado de relación entre el tipo de red y la clase de material predominante (Henaos, 1988; López Cadenas de Llano, 1998; Gaspari, 2002). Cabe mencionar que se denomina red hidrográfica a la totalidad de drenaje natural, permanente o temporal, por el que fluye el escurrimiento superficial.

La densidad de drenaje (Dd) fue establecida por Horton (1932) según el cociente entre la sumatoria de las longitudes de todos los cursos de agua que drenan por la cuenca (Ln) y el área total de la cuenca (A) (López Cadenas de Llano, 1998; Gaspari et al., 2009).

En un principio, y sin tener en cuenta otros factores del medio físico de la cuenca, cuanto mayor sea la densidad del drenaje, más rápida será la respuesta de la cuenca frente a una tormenta, evacuando el agua en menos tiempo. En efecto, al ser la densidad de drenaje alta, una gota deberá recorrer una menor longitud de ladera, con una mayor velocidad de escurrimiento.

Pendiente media del cauce (J): Se deduce a partir del desnivel topográfico sobre el cauce principal y la longitud del mismo (L) (López Cadenas de Llano & Mintegui Aguirre, 1987; López Cadenas de Llano, 1998; Gaspari, 2002). Se expresa en porcentaje.

Tiempo de concentración (Tc): El tiempo que tarda el flujo superficial en contribuir al caudal de salida, desde el punto mas alejado hasta la desembocadura de la cuenca (Chow et al., 1994; Gaspari et al., 2009). El tiempo de concentración también depende de la forma de la cuenca (López Cadenas de Llano & Mintegui Aguirre, 1987).

Kirpich (1940) desarrolló una ecuación empírica, a partir de información antecedente de siete cuencas rurales estadounidenses, con canales bien definidos y pendientes pronunciadas (3 a 10%) (Chow et al., 1994). La Ecuación 3 muestra su expresión de cálculo.

Tc =(0.0078 x L 0.77 )/J 0.385 (Ecuación 3)

Donde Tc: tiempo de concentración (minutos); L: longitud del canal desde aguas arriba hasta la salida (pies) y J: pendiente media del cauce (pie/pie)

La determinación del Tc en la CARSG se determinó por medio de la Ecuación 3, cuya unidad de medida se puede transformar en horas de duración, por la simple división por 60, del resultado de Tc obtenido de la ecuación de Kirpich. Los índices descriptos basaron su determinación sobre datos básicos analizados con SIG, cuyo objetivo final fue la confección en gabinete de la base de datos digital morfológica de la cuenca, formando parte del procedimiento inicial para el diagnóstico morfométrico del proyecto de Pagos por Servicios Ambientales en la cuenca alta del río Sauce Grande describir proyecto.

RESULTADOS Y DISCUSIÓN

Los resultados morfométricos alcanzados en el análisis con SIG permitieron generar cartografía temática descriptiva en la CARSG.

En la Figura 2 se presenta el mapa del modelo digital de elevación (MDE) cuya cota mínima es de 141 m snm y la máxima es de 1214 m snm. En su desembocadura se ubica el dique Paso de las Piedras, con una superficie de embalse de 53.3 km2.

Para el análisis morfométrico inicial se definieron el perfil longitudinal y los perfiles transversales en la cuenca (Figura 2).

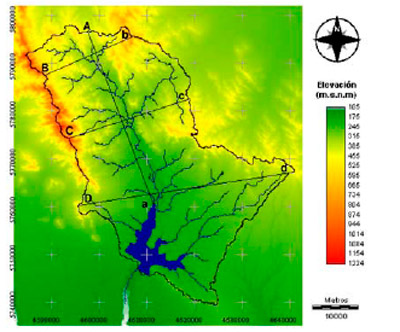Figura 2. Cuenca y drenaje del río Sauce Grande sobre un Modelo digital de elevaciones. Ubicación del perfil longitudinal (A-a) y los transversales (B-b, C-c y D-d).

La Figura 3, representa la distribución altitudinal del perfil longitudinal (A-a) y de los tres transversales, ubicados B-b en la cabecera, el C-c en la parte media y el D-c en la parte baja de la cuenca. En los perfiles transversales se muestran puntos que indican los cursos de agua.

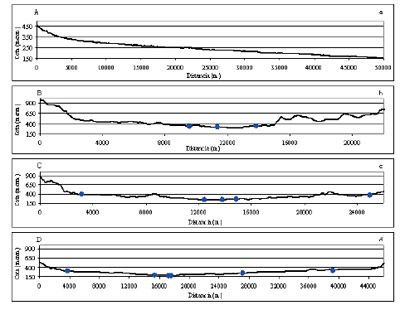Figura 3. Perfiles longitudinal y transversales en la CARSG.

Los resultados morfométricos alcanzados para la cuenca alta del río Sauce Grande se presentan en la Tabla 1.

Los datos calculados a partir de la cartografía y necesarios para el cálculo de los identificadores morfométricos son:el desnivel total de la cuenca (H) 1090 metros, el desnivel del cauce principal es de 282 metros, la longitud en línea recta entre el inicio y final del cauce (Ld) alcanza un valor de 41116 metros. En relación a la longitud total de las curvas de nivel (L) es de 4947.4 km.

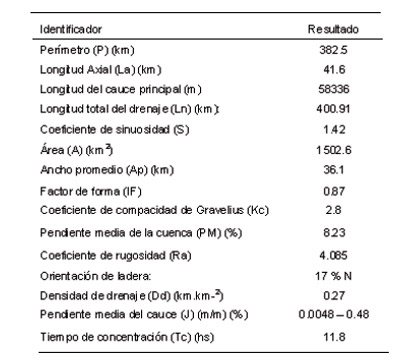Tabla 1. Identificadores de la morfología de CARSG.

Del análisis de los resultados presentados de la Tabla 1 se establece que la cuenca presenta una forma oval – oblonga a rectangular oblonga, que presupone que es poco susceptible a las crecidas, cuyas aguas escurren en general por un solo curso principal.

Continuando con la interpretación de la Tabla 1, el coeficiente de rugosidad, Ra, establece que la cuenca presenta una baja relación entre el desnivel y la densidad de drenaje, generando una alta rugosidad. Los cursos de agua, permanentes y transitorios, de mayor envergadura, favorecidos por el factor topográfico y el coeficiente de rugosidad de la cabecera podrían favorecer la actividad torrencial durante tormentas de alta intensidad en la cabecera. En la parte baja de la cuenca la rugosidad disminuye, y consecuentemente, favoreciendo la disminución de la torrencialidad de las aguas.

En la Figura 4 se presenta el mapa del orden de drenaje de la CARSG donde se identifican cursos de la cabecera con orden 1. El valor de orden 4 es el río principal, siendo el curso de agua cuyo cauce alcanza la máxima magnitud dentro del área ocupada por la cuenca.

La densidad de drenaje natural (Dd), fue relativamente baja, en relación a la superficie de la cuenca (A). En coincidencia

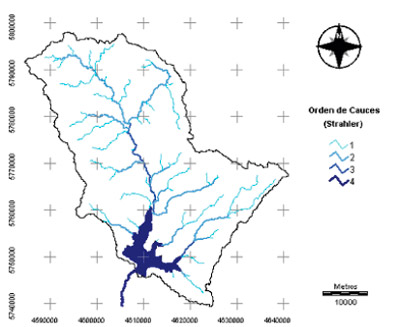Figura 4. Mapa de orden de drenaje en la CARSG.

con lo expresado por Strahler (1957), la presencia de materiales geológicos duros y resistentes en la cabecera originó una baja Dd, y a su vez, en las zonas de derrame, la disposición de materiales permeables, como las arenas y/o gravas, originaron bajas densidades de drenaje, favorecidas por la infiltración. Además se identifica la relación con la distribución de la cubierta vegetal, la topografía y el tipo de suelo. Doffo y González Bonorino (2005) sugieren que cuanto más elongadas son las cuencas, mayor será la tendencia a una alta rugosidad.

La caracterización morfológica de la cuenca permitió identificar la influencia del relieve y morfología sobre su respuesta en un evento aislado al caracterizar el tiempo de concentración (Tc), siendo éste de corta duración.

La curva hipsométrica adimensional para la CARSG se representa en la Figura 5, en comparación con tres curvas hipsométricas correspondientes a cuencas que tienen potenciales evolutivos distintos (Strahler, 1952, 1957; Racca, 2007). La curva superior refleja una cuenca con un gran potencial erosivo, la curva intermedia es característica de una cuenca en equilibrio y la curva inferior es típica de una cuenca sedimentaria. La curva hipsométrica adimensional correspondiente a la cuenca en estudio indica un avanzado grado de desarrollo (cuenca madura), correspondiente en su mayoría a un tipo sedimentario de baja erosionabilidad. Dicha fase puede ser confirmada a través del valor de la integral hipsométrica, ya que su valor es de 21.9%, y, según Strahler (1952) valores inferiores a 30% implican fase de senectud.

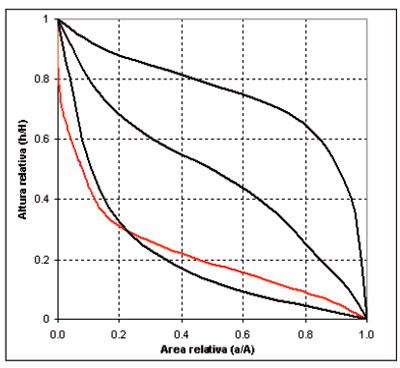Figura 5. Curva hipsométrica adimensional de la CARSG (en rojo).

Los mapas de tipos de relieve y orientación de laderas en la CARSG se presentan en las Figuras 6 y 7 respectivamente.
En la Figura 5 se observa que los relieves predominantes en la CARSG son suaves a lomadas, representando el 72.5% de la superficie de la cuenca. Las áreas planas se distribuyen en un 9.9 % en la parte baja de la cuenca y cercanas a las planicies de inundación, y el 17.5 % restante es de relieve accidentado a fuerte.

La orientación de laderas es similar hacia los cuatro puntos cardinales, expresando una orientación norte en un 17% de su superficie. Presenta un 3% de relieve llano sin una exposición predominante a la escala de estudio.

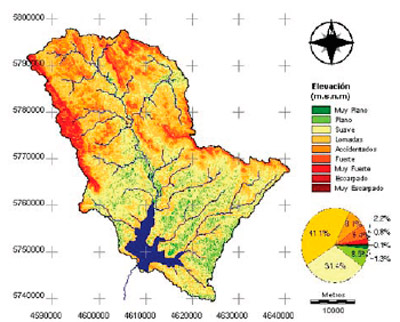Figura 6. Mapa de tipos de relieve en la CARSG.

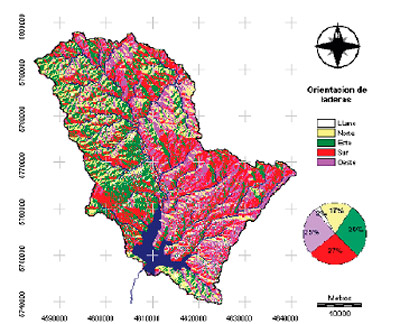Figura 7. Mapa de orientación de laderas en la CARSG.

CONCLUSIONES

Las propiedades morfométricas de la CARSG aportan un marco referencial a los efectos de definir la escala espacial de las investigaciones en ecología fluvial y de esa forma unificar criterios para la delimitación al momento de realizar la colecta, registros y sistematización de información producto de los trabajos empíricos.

Particularmente, la cuenca hidrográfica como unidad de investigación y las propiedades morfométricas de los sistemas fluviales, como marco de referencia, permiten comenzar con la diagramación de un Sistema de Pago por Servicios Ambientales, aportando al ordenamiento territorial.

Los parámetros estudiados proporcionaron información sobre la dinámica espacio temporal del caudal líquido en la cuenca. La cuenca presenta una red de drenaje de cuarto orden. La densidad de la red de drenaje en la CARSG manifiesta la capacidad de entalle de los cauces fluviales y el equilibrio dinámico del sistema acorde a sus condicionantes hidrológicas, geomorfológicas y topográficas, generando posibles áreas de acumulación de escorrentía temporal en épocas de alta intensidad de precipitación, en forma intermitente en la zona de derrame.

El análisis geoespacial logrado con SIG como herramienta de apoyo, constituyó un aporte para dilucidar las variables que actúan a una misma escala espacial y altitudinal sobre la extensión de la red de drenaje y dinámica hídrica y sedimentaria.

En relación a la hipsometría de la cuenca se corroboró un avanzado grado de desarrollo, correspondiente en su mayoría a un tipo sedimentario de baja erosionabilidad. Esto se acompañó con los resultados alcanzados con los parámetros de forma y drenaje. El relieve de la CARSG en su cabecera expresó una forma accidentada a fuerte (17 %), la zona media presentó áreas planas (10 %) y los relieves suaves a lomadas abarcaron aproximadamente el 73 % de la superficie de la cuenca.

Por último, la integración de los parámetros morfométricos en cuencas hidrográficas es un aporte significativo relevante para la consolidación del ordenamiento ambiental, constituyendo una herramienta para la organización de las comunidades y su entorno.

REFERENCIAS BIBLIOGRÁFICAS

Chow VT, Maidment DR & Mays L. 1994. Hidrología Aplicada. Ediciones McGraw-Hill, Colombia: 583 p
Doffo N & G González Bonorino. 2005. Caracterización morfométrica de la cuenca alta del arroyo Las Lajas, Córdoba: Un análisis estadístico. Revista de la Asociación Geológica Argentina, 60 (1): 16-22
Eastman JR. 2006. User Manual Idrisi Andes. Clark University. USA. Disponible en: http://www.clarklabs.org.
Gaspari FJ, Senisterra GE, Delgado MI, Rodríguez Vagaría A & Besteiro S. 2009. Manual de Manejo Integral de Cuencas Hidrográficas. Editorial Autores, 1 ed, La Plata, Argentina: 321p
Gaspari FJ. 2002. Plan de ordenamiento territorial en cuencas serranas degradadas. Aplicación de sistemas de información geográfica. Huelva. España. Ediciones Cooperativas, Buenos Aires: 179 p
Henaos JE. 1988. Introducción al manejo de cuencas hidrográficas. Universidad Santo Tomás, Centro de enseñanza desescolarizada, Bogotá, Colombia: 396 p
Horton RE. 1932. Drainage-basin characteristics. Transactions American Geophysical Union. Washington, USA: 13: 350-361
Instituto Geográfico Militar (IGM). Cartas topográficas. República Argentina. Escala 1:50.000. Tornquist (3963-5-2), 1968; Sierra de la Ventana (3963-6-1), 1972; Peralta (3963-6-2), 1972; Tres Picos (3963-5-4), 1967; Saldungaray (3963-6-3) 1971; Estancia las Águilas (3963-6-4), 1971; Cabildo (3963-12-1), 1971; Lartigau (3963-12-2), 1970. Buenos Aires, Argentina.
Instituto Nacional de Tecnología Agropecuaria (INTA). 1989. Mapa de Suelos de la Provincia de Buenos Aires, escala 1:500.000. Ediciones INTA, Buenos Aires, Argentina: 473 p
Jardí M. 1985. Forma de una cuenca de drenaje. Análisis de las variables morfométricas que nos la definen. Revista de Geografía, Barcelona, España: 19: 41-68
Kirpich ZP. 1940. Time of concentration of small agricultural watersheds. Civil Engineering, New York, USA, 10 (6): 362 p Llamas J. 1993. Hidrología general: principios y aplicaciones. Servicio Editorial de la Universidad del País Vasco, Bilbao, España : 635 p
López Cadenas de Llano F & Mintegui Aguirre JA. 1987. Hidrología de superficie. Editorial Salazar. Escuela de Técnica Superior de Ingenieros de Montes, Madrid, España: 222 p
López Cadenas de Llano F. 1998. Restauración Hidrológica Forestal de cuencas y Control de la Erosión. Ingeniería Medioambiental, TRAGSATEC, Ministerio de Medio Ambiente. Editorial Mundi Prensa, Madrid, España: 945 p
Luque JA, Paoloni JD & Bonorino GA. 1979. Estudio geológico e hidrogeológico de la cuenca del Río Sauce Grande. Publicación interna del Departamento de Ciencias Agrarias y de Ciencias Naturales de la Universidad Nacional del Sur, Serie Hidrología. Bahía Blanca, Argentina, 3: 64 p
Morisawa ME. 1985. Rivers: forms and process. Longman, London, England: 222 p
Mintegui Aguirre JA & López Unzú F. 1990. La Ordenación Agrohidrológica en la Planificación. Servicio Central de Publicaciones del Gobierno Vasco, Bilbao, España: 306 p
Patton P. 1998. Drainage basin morphometry and floods. P 51-64 En:Baker V, Kochel C & P Patton (eds) Flood geomorphology. John Wiley & Sons
Rabassa J. 1982. Variación regional y significado geomorfológico de la densidad de drenaje en la cuenca del río Sauce Grande, Provincia de Buenos Aires. Revista de la Asociación Geológica Argentina, 37 (3): 268-284
Racca JMG. 2007. Análisis hipsométrico, frecuencia altimétrica y pendientes medias a partir de modelos digitales del terreno. Boletín del Instituto de Fisiografía y Geología. Rosario, Argentina, 77 (1-2): 31-38
Strahler AN. 1952. Hypsometric (area-altitude) analisys of erosional topography. Bulletin of the Geological Society of America, 63: 1117 – 1142
Strahler AN. 1957. Quantitative analysis of watershed geomorphology. Transactions American Geophysical Union, 38 (6): 913 – 925
Strahler AN. 1964. Quantitative geomorphology of drainage basins and channel networks. Section 4-II of Handbooks of Applied Hydrology. Mc Graw-Hill Book Co, New York, USA

Por: Fernanda J Gaspari, Alfonso M Rodríguez Vagaría, Gabriela E Senisterra,
Gerardo Denegri, María I Delgado, Sebastián Besteiro
Fuente: Sedici

VER ARCHIVO DE ARTÍCULO