NTP 333: Análisis probabilístico de riesgos: Metodología del «Árbol de fallos y errores»
|
NTP 333: Análisis probabilístico de riesgos: Metodología del «Árbol de fallos y errores»
Redactor: Tomás Piqué Ardanuy Ingeniero Técnico Químico Licenciado en Derecho |
||||||||||||||||||||
Fuente: Ministerio de Trabajo y Asuntos Sociales de España
Introducción
Habida cuenta que las técnicas evolucionan rápida y continuamente y que la complejidad de los sistemas e instalaciones industriales es creciente, resulta cada vez más limitado establecer programas de seguridad únicamente en base a los conocimientos adquiridos o por extrapolación de situaciones similares.
Ciertamente, los conocimientos y la experiencia permiten establecer reglas generales, apoyándose en normas y reglamentaciones que se deben cumplir, pero la seguridad a exigir e implantar en una instalación o en un proceso concreto intrínsecamente peligroso precisa de una evaluación puntual de los peligros existentes.
Esta evaluación, que conocemos como «análisis de riesgos», nos habrá de permitir identificar los riesgos y evaluarlos cual cualitativamente y, si cabe, también cuantitativamente.
Ello no es tarea fácil cuando el riesgo viene determinado por diversidad de factores de riesgo o de posibles fallos en su mayoría concatenados entre sí. Es imprescindible discernir y considerar todos los fallos significativos para estimar sus consecuencias y la probabilidad de acontecimiento, para finalmente conocer el riesgo de que sucedan determinados accidentes. Y a resultas de ello establecer un programa de mejoras y de control del riesgo.
Esta NTP tiene por objeto dar a conocer a nivel introductorio la Metodología del «Árbol de fallos y errores» como técnica para el «análisis de riesgos» que nos ha de facilitar la determinación del riesgo propio de cada situación, cuando se conjuga una diversidad de fallos a estudiar. Aunque la técnica se aplica fundamentalmente para el análisis de riesgos a partir de acontecimientos finales muy graves que pueden suceder en procesos industriales y que, por supuesto, se trata de evitar, también resulta útil en situaciones en las que se pretende analizar «hacia atrás» el origen de determinados sucesos indeseados.
Antecedentes del análisis por el «árbol de fallos y errores»
El método de análisis del «Árbol de Fallos» (FTA: Fault Tree Analysis) (en esta NTP hablamos de «Árbol de fallos y errores» para permitir diferenciar terminológicamente los fallos de los componentes de las instalaciones de los errores en el comportamiento humano) fue concebido y utilizado por vez primera en 1962 por H. A. Watson, de Bell Telephone Laboratories, en relación con un contrato de Air Force para evaluar las condiciones de seguridad de los sistemas de tiro de los misiles ICBM Minuteman.
A partir de ese momento, esta técnica de análisis de riesgos ha sido profusamente utilizada y perfeccionada por parte de instalaciones nucleares, aeronáuticas y espaciales, extendiéndose después su empleo para la evaluación de riesgos a las industrias electrónica, química, petroquímica, etc.
Actualmente, las graves catástrofes industriales que han ocurrido en el mundo (Feyzin, Flixborough, Bophal, Chernobil, etc.) han sensibilizado a la opinión pública, motivando a las autoridades a legislar sobre el tema, tanto a nivel de la Unión Europea como a nivel
interno de cada país. Así, la «Directiva Seveso» y sus posteriores modificaciones transpuestas a nuestra legislación interna obligan a ciertas industrias a realizar estudios de sus riesgos potenciales capaces de actualizarse en accidentes mayores.
Si para la identificación y evaluación cualitativa de riesgos en procesos químicos es el Hazop (Análisis funcional de operabilidad) el procedimiento más utilizado (NTP 238-1989), para su cuantificación el método del «árbol de fallos y errores» expuesto en la presente NTP es un método clave, aunque su aplicación legal queda limitada en nuestra reglamentación sobre prevención de accidentes mayores a cuando la autoridad competente lo exija.
Descripción del método
Se trata de un método deductivo de análisis que parte de la previa selección de un «suceso no deseado o evento que se pretende evitar», sea éste un accidente de gran magnitud (explosión, fuga, derrame, etc.) o sea un suceso de menor importancia (fallo de un sistema de cierre, etc.) para averiguar en ambos casos los orígenes de los mismos.
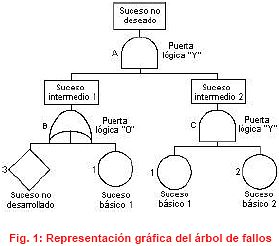 |
Seguidamente, de manera sistemática y lógica se representan las combinaciones de las situaciones que pueden dar lugar a la producción del «evento a evitar», conformando niveles sucesivos de tal manera que cada suceso esté generado a partir de sucesos del nivel inferior, siendo el nexo de unión entre niveles la existencia de «operadores o puertas lógicas». El árbol se desarrolla en sus distintas ramas hasta alcanzar una serie de «sucesos básicos», denominados así porque no precisan de otros anteriores a ellos para ser explicados. También alguna rama puede terminar por alcanzar un «suceso no desarrollado» en otros, sea por falta de información o por la poca utilidad de analizar las causas que lo producen.
Los nudos de las diferentes puertas y los «sucesos básicos o no desarrollados» deben estar claramente identificados.
Estos «sucesos básicos o no desarrollados» que se encuentran en la parte inferior de las ramas del árbol se caracterizan por los siguientes aspectos:
- Son independientes entre ellos.
- Las probabilidades de que acontezcan pueden ser calculadas o estimadas.
Para ser eficaz, un análisis por árbol de fallos debe ser elaborado por personas profundamente conocedoras de la instalación o proceso a analizar y que a su vez conozcan el método y tengan experiencia en su aplicación; por lo que, si se precisa, se deberán constituir equipos de trabajo pluridisciplinarios (técnico de seguridad, ingeniero del proyecto, ingeniero de proceso, etc.) para proceder a la reflexión conjunta que el método propicia.
Desarrollo del árbol
Prefijado el «evento que se pretende evitar» en el sistema a analizar, se procede descendiendo escalón a escalón a través de los sucesos inmediatos o sucesos intermedios hasta alcanzar los sucesos básicos o no desarrollados que generan las situaciones que, concatenadas, contribuyen a la aparición del «suceso no deseado».
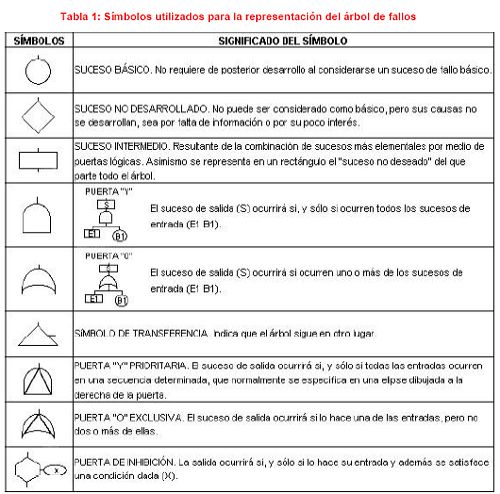
Para la representación gráfica de los árboles de fallos y con el fin de normalizar y universalizar la representación se han elegido ciertos símbolos que se representan en la Tabla 1.
 |
Si alguna de las causas inmediatas contribuye directamente por sí sola en la aparición de un suceso anterior, se conecta con él mediante una puerta lógica del tipo «O».
Por ejemplo:
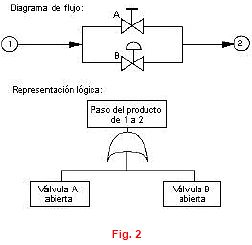
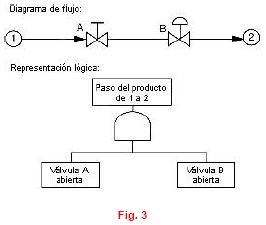
En el diagrama de flujo, el producto pasará del punto 1 al punto 2 si está abierta la válvula manual A o si está abierta la válvula neumática B, y su representación lógica es la especificada en la figura.
 |
Si son necesarias simultáneamente todas las causas inmediatas para que ocurra un suceso, entonces éstas se conectan con él mediante una puerta lógica del tipo «Y».
Por ejemplo:
En el diagrama de flujo representado, tienen que estar abiertas simultáneamente las válvulas A y B para que pase el producto del punto 1 al 2, y su representación lógica es la especificada en la figura.
 |
Procediendo sucesivamente de esta forma, se sigue descendiendo de modo progresivo en el árbol hasta llegar a un momento en que, en la parte inferior de las distintas ramas de desarrollo, nos encontramos con sucesos básicos o no desarrollados. Habremos entonces completado la confección del árbol de fallos y errores.
Explotación del árbol
La explotación de un árbol de fallos puede limitarse a un tratamiento «cualitativo» o acceder a un segundo nivel de análisis a través de la «cuantificación» cuando existen fuentes de datos relativas a las tasas de fallo de los distintos componentes.
Evaluación cualitativa
Consiste en analizar el árbol sobre el plano de su estructura lógica para poder determinar las combinaciones mínimas de sucesos básicos que hagan que se produzca el suceso no deseado o evento que se pretende evitar (noción de «conjunto mínimo de fallos»).
Además, la estructura lógica de un árbol de fallos permite utilizar el álgebra de Boole, traduciendo esta estructura a ecuaciones lógicas. Para ello se expone muy brevemente tal sistema de equivalencia lógica:
- Una puerta «0» equivale a un signo «+», no de adición sino de unión en teoría de conjuntos.
- Una puerta «Y» equivale a un signo «.» equivalente a la intersección.
Algunas de las leyes y propiedades básicas del álgebra de Boole más importantes son:
- Propiedad conmutativa:
x + y = y + xX · y = y · x - Propiedad asociativa:
x + (y + z) = (x + y) + zx · (y · z) = (x · y) · z - Propiedad distributiva:
x · (y + z) = x · y + x · z(x + y) · z = x · y + x · z - Propiedad idempotente:
x · x = xx + x = x - Ley de absorción:
x · (x + y) = xx + x · y = x
De ello se extraen las siguientes consecuencias:
- Transformar el árbol de fallos en una función lógica.
- La posibilidad de simplificar la función lógica del árbol gracias a la constatación de falsas redundancias. La reducción de falsas redundancias (reducción booleana) consiste en simplificar ciertas expresiones booleanas y consecuentemente los elementos de estructura que las mismas representan.
Lo anterior resalta la importancia de identificar durante el análisis, además de los fallos individuales de los componentes, los posibles fallos debidos a una causa común o la determinación de los componentes que fallan del mismo modo.
Para la resolución de árboles de fallos se realizan los siguientes pasos:
- Identificación de todas las puertas lógicas y sucesos básicos.
- Resolución de todas las puertas en sus sucesos básicos.
- Eliminación de los sucesos repetidos en los conjuntos de fallo: aplicación de la propiedad idempotente del álgebra de Boole.
- Eliminación de los conjuntos de fallo que contengan a su vez conjuntos de fallo más pequeños, es decir, determinación de entre todas las combinaciones posibles, los conjuntos mínimos de fallo: aplicación de la ley de absorción del álgebra de Boole.
A título de ejemplo, en el caso de árboles sencillos, los conjuntos mínimos de fallos se pueden obtener sustituyendo las puertas «O» por sus entradas en las filas de una matriz y las de las puertas «Y» en columnas. Fig. 4
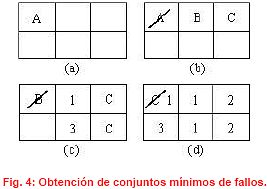 |
Se trata de ir descendiendo en el árbol para su resolución eliminando y sustituyendo los sucesivos símbolos de identificación de las puertas hasta obtener las diferentes combinaciones de fallos primarios identificados.
De la resolución del árbol de fallos, obtenemos:
- Vías secuenciales de fallos básicos generadores del acontecimiento final: 1.2 y 1.2.3.
- Conjunto mínimo de fallos que son necesarios para que se produzca el acontecimiento final: 1.2.
La vía 1.2.3 en realidad es la misma que la 1.2, ya que el evento ya sucede con la simultaneidad de los fallos 1 y 2 sin necesidad de que acontezca el fallo 3, con lo que el conjunto mínimo de fallos es el 1.2.
En la práctica, los árboles suelen ser bastante más complejos y la resolución en conjuntos mínimos de fallos es más dificultosa, por lo que se suele acudir a paquetes de software que resuelven los árboles tanto cualitativamente como cuantitativamente.
Asimismo, la utilización de la informática permite efectuar simulaciones que nos permiten examinar las diferentes combinaciones existentes y resumir el árbol en los conjuntos mínimos de fallos.
Evaluación cuantitativa
Precisa conocer la indisponibilidad o probabilidad de fallo de aquellos sucesos que en el árbol se representan en un círculo (sucesos básicos) y determinar valores probabilísticos de fallo a aquellos sucesos que se representan en un rombo (sucesos no desarrollados).
Según el modo en que ha fallado el componente, se calcula la probabilidad de fallo del mismo en función de la tasa de fallo que se puede obtener en bancos de datos y, fundamentalmente, de la propia experiencia. Existe, asimismo, información que nos proporciona datos estimativos sobre tasas de errores humanos que permite asignar valores probabilísticos a su ocurrencia.
El conocimiento de los valores de probabilidad de los sucesos primarios (básicos o no desarrollados) permite:
- Determinar la probabilidad global de aparición del «suceso no deseado» o «evento que se pretende evitar».
- Determinar las vías de fallo más críticas, es decir, las más probables entre las combinaciones de sucesos susceptibles de ocasionar el «suceso no deseado».
Para la valoración de la probabilidad global de aparición del «suceso no deseado» se realizan los siguientes pasos:
- Se asignan valores probabilísticos a los sucesos primarios.
- Se determinan las combinaciones mínimas de sucesos primarios cuya ocurrencia simultánea garantiza la aparición del «suceso no deseado»: establecimiento de los «conjuntos mínimos de fallos».
- Se calcula la probabilidad de cada una de las vías de fallo representada por los conjuntos mínimos de fallos, la cual es igual al producto (intersección lógica en álgebra de Boole) de las probabilidades de los sucesos primarios que la componen.
- Se calcula la «probabilidad de que se produzca el «acontecimiento final», como la suma de las probabilidades (unión lógica de todos los N conjuntos mínimos de fallo en álgebra de Boole) de los conjuntos mínimos de fallo, como límite superior, ya que matemáticamente debería restarse la intersección de éstos.
A título de ejemplo, si en el caso del árbol representado en la fig. 1 asignamos valores medios de probabilidades de fallo a los sucesos primarios:
- P 1 = 5 · 10 -3; P 2 = 6 · 10 -2; P 3 = 10 -3
- Conjunto mínimo de fallos: P 1 y P 2
- Pvía(1)= P 1 · P 2 = 5 · 10 -3 x 6 · 10 -2 = 300 · 10 -6
- Probabilidad de acontecimiento final: PAF = P 1 · P 2 = 300 · 10 -6
En este caso coincide con la probabilidad del conjunto mínimo de fallos ya que éste es único. En el supuesto que se plantea a continuación, en que el árbol que se desarrolla es ligeramente más complejo, se observará cómo se calcula la PAF a partir de la existencia de varios conjuntos mínimos de fallos.
Ejercicio de aplicación del método «árbol de fallos y errores»
|
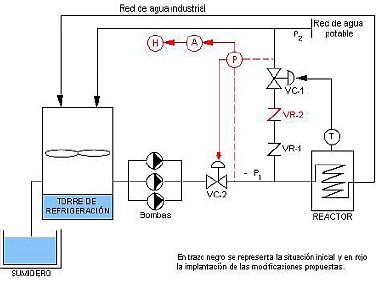
«En una empresa química existe una nave de producción en la cual el reactor es refrigerado por una red de agua industrial en circuito cerrado», siendo ésta enfriada por una torre de refrigeración tal y como se muestra en el esquema 1.
Esquema 1: Representación del proceso. En trazo negro se representa la situación inicial y en rojo la implantación de las modificaciones propuestas Hay veces en verano que la temperatura del agua de este circuito no es suficientemente baja y se debe enfriar complementariamente con la red de agua potable, mediante la apertura de la válvula VC-1 que es accionada neumáticamente a través del termostato T. La empresa se ha planteado con preocupación que la red de agua industrial pudiera contaminar el agua potable, por las consecuencias que de ello podrían derivarse. (La interconexión de ambas redes de agua está explícitamente prohibida en la 0.G.S.H.T. en su art. 38.4, por lo que este enunciado contempla un supuesto teórico cuyo único fin es el de facilitar la comprensión del método y la reflexión sobre los resultados del análisis probabilístico.) Obviamente, para que el agua industrial entrase en la canalización de agua potable debería ser la presión P-1 mayor que P-2 (situación que no se da en condiciones habituales), tendría que fallar la válvula antirretorno VR-1 y fallar la válvula VC-1, salvo en períodos calurosos en que VC-1 está abierta. En el análisis de este supuesto se considera que la válvula de control VC-1 se encuentra cerrada. Obviamente, cuando la válvula de control está abierta por requerimiento del proceso, en la elaboración del árbol se deberían eliminar los diferentes modos de fallo de este elemento.» |
En esta situación, analizamos la probabilidad de contaminación de la red de agua potable cuando accidentalmente la presión P-1 supera a la presión P-2, mediante la elaboración del correspondiente árbol de fallos; considerando para la realización de este ejercicio las siguientes probabilidades de fallo de los diferentes elementos:
Fallo de válvula de retención VR por retroceso del fluido 10-2
Fallo de estanqueidad de VC en posición de cierre 10 -3
Posibilidad de bloqueo de las válvulas neumáticas VC al abrir o cerrar 10-3
Fallo del termostato de regulación de VC 10-3
Fallo de transmisión de señal del termostato o presostato 10-4
Fallo presostato 10-3
Fallo señal acústica de alarma 10-2
Probabilidad de no actuación correcta ante alarma 10-2
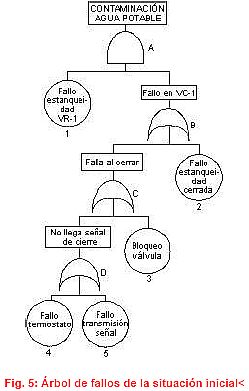 |
El cálculo de los conjuntos mínimos de fallo y de la probabilidad de contaminación del agua potable es:
 |
Con lo que la probabilidad del suceso no deseado, es decir, de contaminación del agua potable es:
P = P (1,2) + P(1,3) + P (1,4) + P(1,5) =
= P 1 P 2 +P 1 P 3 + P 1P 4 +P 1 P 5 = 3, 1 · 10 -5
Del análisis de la situación actual de la instalación observamos que la probabilidad de contaminación de la red de agua potable cuando P1 > P2 es de 3,1 · 10 -5 y en la situación en que la válvula de control VC-1 está abierta la probabilidad de contaminación del agua potable es la de que falle la válvula de retención VR-1, es decir, P = 10 -2; siendo ambas probabilidades no aceptables ante las posibles consecuencias a que daría lugar en caso de producirse la contaminación.
| «Ante ello, valoramos como variaría tal probabilidad de contaminación incorporando a la instalación actual una segunda válvula de retención así como un presostato que actúe, cuando P-1 se aproxime a P-2, sobre la válvula VC2 dándole orden de cierre y, a su vez, al activarse dé una alarma acústica en sala de control, a fin de que pudiera actuarse manualmente sobre VC-2 en caso de fallo del cierre neumático.
Con el cierre de VC-2 se desconecta la alarma y el consiguiente incremento de temperatura activaría el termostato T accionando la apertura de VC-1. La red de agua potable garantiza suficiente caudal para mantener refrigerado el reactor.» |
Analizamos en esta nueva situación como varía la probabilidad de contaminación de la red de agua potable, mediante la elaboración de un nuevo árbol de fallos en el que se contemplan las variaciones simuladas.
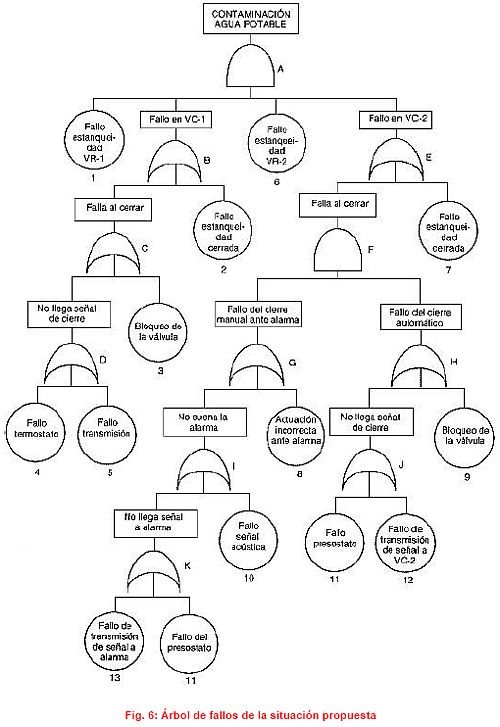 |
El cálculo de los conjuntos mínimos de fallo y de la probabilidad de contaminación del agua potable se indica en la figura 7.
 |
Obtendremos la probabilidad de contaminación del agua potable mediante la suma de las probabilidades de ocurrencia de los conjuntos mínimos de fallo, dando un valor de 6,2685 · 10 -10. En las situaciones en que VC-1 está abierta (período muy caluroso), la probabilidad se incrementa hasta un valor de 2,0221 · 10 -7.
En esta nueva situación, se observa como, con la incorporación de unos determinados elementos básicos de seguridad, se ha obtenido una importante mejora en cuanto a la fiabilidad de la instalación en lo referente a la probabilidad de contaminación del agua potable. Tengamos en cuenta que una probabilidad de daño inferior a 10 -1 puede considerarse indicativa de un hecho de materialización remota, en cuyo entorno podría encontrarse la frontera de aceptabilidad social de las situaciones de riesgo de graves consecuencias.
De la resolución de este supuesto en sus dos situaciones, la inicial y la propuesta de modificación, se desprende cómo esta metodología de análisis permite, a partir de una situación dada, establecer simulaciones que nos permiten conocer y valorar como va evolucionando la seguridad de la instalación y, en consecuencia, adoptar las soluciones que nos permitan alcanzar unas cotas de seguridad técnica y socialmente aceptables y asimismo facilita la justificación de las inversiones en seguridad, puesto que permite conocer el grado de mejora que se obtendrá con la implantación de tales medidas.
Si bien es cierto que la aplicación de esta metodología presenta ciertas dificultades, tales como que exige un alto grado de conocimientos y experiencia tanto de las instalaciones a analizar como del propio método y que precisa disponer de bases de datos propios a fin de superar la incertidumbre que genera la asignación de valores de probabilidad de fallo a los componentes de la instalación que se analiza; hay que considerar que el esfuerzo necesario para realizar los análisis de riesgos cualitativos y cuantitativos queda ampliamente compensado no sólo por la mejora final de la seguridad del sistema, sino, además, por el enriquecimiento del equipo analizador en el conocimiento exhaustivo del funcionamiento del proceso y de los diferentes modos de fallo resultantes de las posibles alteraciones de las múltiples variables que condicionan el sistema.
Bibliografía
(1) FAVARO, M et alt. Bilan des méthodes d’analyse a priori des risques Nancy, INRS, 1990, Cahiers de notes documentaires nº 139
(2) RAMOS ANTÓN, ARISTIDES Procedimiento para la valoración cuantitativa de los riesgos. Métodos de los árboles de fallos Madrid, COASHIQ, 1990